
 如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=2$\sqrt{3}$,AB=AD=2,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=2$\sqrt{3}$,AB=AD=2,点F是PB的中点,点E在边BC上移动.分析 (Ⅰ)利用三角形中位线的性质可得,当点E在BC的中点时,有EF∥平面PAC;
(Ⅱ)由题意可得,BC⊥平面PAB,在Rt△PAB中,由PA=2$\sqrt{3}$,AB=2,得PB=4,再结合F为PB的中点,得到三角形ABF为正三角形,找出二面角的平面角,通过求解直角三角形求得BE,再由等积法求得三棱锥A-EBF的体积.
解答 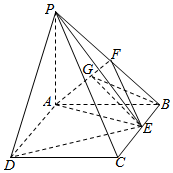 解:(Ⅰ)当点E在BC的中点时,有EF∥平面PAC
解:(Ⅰ)当点E在BC的中点时,有EF∥平面PAC
事实上,若E为BC中点,又点F是PB的中点,
∴EF为△BPC的中位线,则EF∥PC,
∵PC?面PAC,EF?面PAC,
∴由线面平行的判定可得,EF∥平面PAC;
(Ⅱ)由PA⊥平面ABCD,可得平面PAB⊥平面ABCD,
又四边形ABCD为矩形,即BC⊥AB,∴BC⊥平面PAB,
在Rt△PAB中,由PA=2$\sqrt{3}$,AB=2,得PB=4,
由F为PB的中点,可得BF=2,
取AF中点G,连接BG,则BG⊥AF,
再连接EG,有EG⊥AF,
∴∠EGB为二面角E-AF-B的平面角为30°,
在正三角形ABF中,由边长为2,可得BG=$\sqrt{3}$,
在Rt△EBG中,可得$tan30°=\frac{BE}{BG}=\frac{BE}{2}$,则BE=$\frac{2\sqrt{3}}{3}$.
∴${V}_{A-EBF}={V}_{E-BAF}=\frac{1}{3}×\frac{1}{2}×2×\sqrt{3}×\frac{2\sqrt{3}}{3}$=$\frac{1}{6}$.
点评 本题考查直线和平面平行的判定,考查棱锥体积的求法,训练了等积法求多面体的体积,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $({\frac{4}{3},2}]$ | B. | $({-∞,0})∪({\frac{4}{3},+∞})$ | C. | (-∞,0) | D. | $({-∞,0})∪({\frac{4}{3},2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | ±$\frac{2\sqrt{2}}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
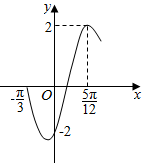 函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )
函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )| A. | $2\;,\;-\frac{π}{3}$ | B. | $2\;,\;-\frac{π}{6}$ | C. | $4\;,\;-\frac{π}{6}$ | D. | $4\;,\;\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 零件数x(个) | 2 | 3 | 4 | 5 |
| 加工时间y(min) | 26 | 39 | 49 | 54 |
| A. | 63.6min | B. | 65.5min | C. | 67.7min | D. | 72.0min |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值为1,图象关于直线x=$\frac{π}{2}$对称 | B. | 在(0,$\frac{π}{4}$)上单调递减,为奇函数 | ||
| C. | 在(-$\frac{3π}{8}$,$\frac{π}{8}$)上单调递增,为偶函数 | D. | 周期为π,图象关于点($\frac{3π}{8}$,0)对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com