
| A. | 2 | B. | 3 | C. | 2$\sqrt{2}$-1 | D. | 4 |
分析 把极坐标方程化为直角坐标方程,求出圆心到直线的距离d,进而得出最小距离=d-r.
解答 解:由ρcosθ-ρsinθ+5=0化为直角坐标方程:x-y+5=0,
ρ=2sinθ即ρ2=2ρsinθ,化为直角坐标方程:x2+y2=2y,
配方为:x2+(y-1)2=1,圆心C(0,1),半径r=1.
圆心C到直线的距离d=$\frac{|0-1+5|}{\sqrt{2}}$=2$\sqrt{2}$>1,
∴A,B两点之间距离的最小值=d-r=2$\sqrt{2}$-1.
故选:C.
点评 本题考查了极坐标方程化为直角坐标方程、圆的标准方程、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
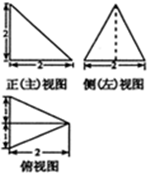
| A. | $\frac{4}{3}$ | B. | 1 | C. | $\frac{5}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
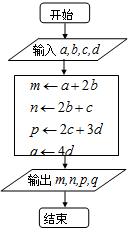 为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则如图所示,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )
为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则如图所示,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )| A. | 4,6,1,7 | B. | 7,6,1,4 | C. | 6,4,1,7 | D. | 1,6,4,7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 保留 | 不支持 | |
| 20岁以下 | 800 | 450 | 200 |
| 20岁以上(含20岁) | 100 | 150 | 300 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com