
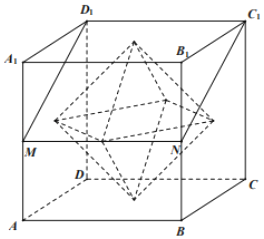
【题目】如图,点M,N分别为正方体ABCD﹣A1B1C1D1的棱AA1,BB1的中点,以正方体的六个面的中心为顶点构成一个八面体,若平面D1MNC1将该八面体分割成上、下两部分的体积分别为V1、V2,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
如图,先作出平面![]() 截八面体的截面为
截八面体的截面为![]() ,建立空间直角坐标系,用点
,建立空间直角坐标系,用点![]() 到平面
到平面![]() 的距离
的距离![]() 为向量
为向量![]() 在法向量
在法向量![]() 上的投影的长,再计算两部分的体积,得到体积之比,得到答案.
上的投影的长,再计算两部分的体积,得到体积之比,得到答案.
正方体的六个面的中心为顶点构成的八面体中中间和上方的顶点分别为![]()
如图,分别过![]() 作侧棱的平行线,
作侧棱的平行线,
分别![]() 交于点
交于点![]() ,分别
,分别![]() 交于点
交于点![]() ,得到矩形
,得到矩形![]() .
.

由题意有![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
在矩形![]() 中,
中,![]() 分别交
分别交![]() 于点
于点![]() ,则
,则![]() 分别为
分别为![]() 的中点,
的中点,
![]() 平面
平面![]() ,所以,
,所以,![]() 平面
平面![]() .
.
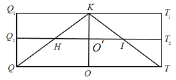
将平面![]() 延展与
延展与![]() 交于
交于![]() 点. 所以平面
点. 所以平面![]() 截八面体的截面为
截八面体的截面为![]() .
.
显然![]() 与
与![]() 相交于
相交于![]() 的中点,设为
的中点,设为![]() .则
.则![]() 三点共线.
三点共线.
在![]() 中,过
中,过![]() 作
作![]() ,如图,可得
,如图,可得![]() 为
为![]() 的一个三等分点.
的一个三等分点.

设正方体的棱长为2,则![]() .
.
以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系
P(-1,0,0),R(1,0,0),Q(0,-1,0),
![]()
![]()
![]()
设平面![]() 的法向量为
的法向量为![]() .
.
则 ,即
,即 ,取
,取![]() 则
则![]()
则点![]() 到平面
到平面![]() 的距离
的距离![]() 为向量
为向量![]() 在法向量
在法向量![]() 上的投影的长.
上的投影的长.
所以
又![]()

![]()
![]()
所以八面体在平面平面![]() 下方的部分的体积为
下方的部分的体积为![]()
所以![]()
故选:A



 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且an=![]() (3n+Sn)对一切正整数n成立
(3n+Sn)对一切正整数n成立
(I)证明:数列{3+an}是等比数列,并求出数列{an}的通项公式;
(II)设![]() ,求数列
,求数列![]() 的前n项和Bn;
的前n项和Bn;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴正半轴建立直角坐标系
轴正半轴建立直角坐标系![]() ,直线
,直线![]() 经过点
经过点![]() 且倾斜角为
且倾斜角为![]() .
.
![]() 求圆
求圆![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的参数方程;
的参数方程;
![]() 已知直线
已知直线![]() 与圆
与圆![]() 交与
交与![]() ,
,![]() ,满足
,满足![]() 为
为![]() 的中点,求
的中点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班要从6名男生4名女生中选出5人担任5门不同学科的课代表,请分别求出满足下列条件的方法种数![]() 结果用数字作答
结果用数字作答![]() .
.
(1)所安排的男生人数不少于女生人数;
(2)男生甲必须是课代表,但不能担任语文课代表;
(3)女生乙必须担任数学课代表,且男生甲必须担任课代表,但不能担任语文课代表.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|y=lg(x-![]() )},B={x|
)},B={x|![]() -cx<0,c>0},若AB,则实数c的取值范围是( )
-cx<0,c>0},若AB,则实数c的取值范围是( )
A.(0,1]B.[1,+∞)
C.(0,1)D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过抛物线C:y2=2px(p>0)的准线l上的点M(﹣1,0)的直线l1交抛物线C于A,B两点,线段AB的中点为P.
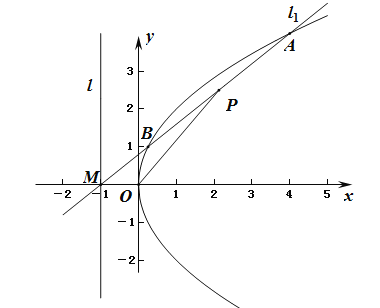
(Ⅰ)求抛物线C的方程;
(Ⅱ)若|MA||MB|=λ|OP|2,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空间四边形ABCD的对棱AD,BC成60°的角,且AD=a,BC=b,平行于AD与BC的截面分别交AB,AC,CD,BD于E、F、G、H,则截面EFGH面积的最大值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com