
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)答案不唯一,具体见解析(Ⅱ)![]() 或
或![]()
【解析】
(Ⅰ)求出函数的导数,通过讨论![]() 的范围,求出函数的单调区间即可。
的范围,求出函数的单调区间即可。
(Ⅱ)由于![]() 时,
时,![]() ,若要
,若要![]() 使得
使得![]() 成立,只需
成立,只需![]() 时,
时,![]() 成立,利用导数讨论
成立,利用导数讨论![]() 的最大值和
的最大值和![]() 的最小值,即可求出实数
的最小值,即可求出实数![]() 的取值范围。
的取值范围。
(Ⅰ)由题可得![]() 的定义域为
的定义域为![]() ,
,![]()
![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,或
,或![]() ,
,![]() ,解得
,解得![]() ,
,
∴![]() 在
在![]() ,
,![]() 上是增函数,在
上是增函数,在![]() 上是减函数;
上是减函数;
当![]() 时,
时,![]() ,解得
,解得![]() ,或
,或![]() ,
,![]() ,解得
,解得![]() ,
,
∴![]() 在
在![]() ,
,![]() 上是增函数,在
上是增函数,在![]() 上是减函数;
上是减函数;
当![]() 时,
时,![]() 恒成立,且只在
恒成立,且只在![]() 时
时![]() ,∴
,∴![]() 在
在![]() 上是增函数.
上是增函数.
(Ⅱ)![]() 时,
时,![]() ,
,
若要![]() 使得
使得![]() 成立,
成立,
只需![]() 时,
时,![]() 成立,
成立,
由(Ⅰ)知当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上是减函数,
上是减函数,![]() ,
,
![]() ,对称轴
,对称轴![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,![]() ,
,
![]() ,解得
,解得![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
![]() ,
,![]() ,
,
整理得![]() ,∵
,∵![]() ,∴只需
,∴只需![]() ,
,
令![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是增函数,又
上是增函数,又![]() ,∴
,∴![]() 时,
时,![]() ,∴
,∴![]() .
.
当![]() 时,
时,![]() 在
在![]() 上是减函数,
上是减函数,![]() ,
,
![]() ,解得
,解得![]() ,
,
综上所述,![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
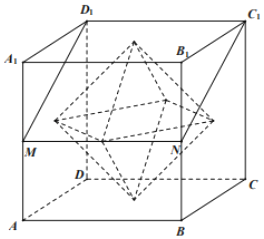
【题目】如图,点M,N分别为正方体ABCD﹣A1B1C1D1的棱AA1,BB1的中点,以正方体的六个面的中心为顶点构成一个八面体,若平面D1MNC1将该八面体分割成上、下两部分的体积分别为V1、V2,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
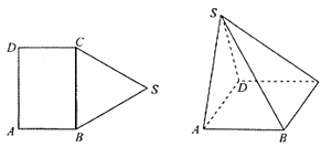
【题目】如图,五边形![]() 中,四边形
中,四边形![]() 为长方形,
为长方形,![]() 为边长为
为边长为![]() 的正三角形,将
的正三角形,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 在平面
在平面![]() 上的射影恰好在
上的射影恰好在![]() 上.
上.
(Ⅰ)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成二面角的余弦值的绝对值.
所成二面角的余弦值的绝对值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点在原点,焦点![]() 在
在![]() 轴的正半轴,且过点
轴的正半轴,且过点![]() ,过
,过![]() 的直线交抛物线于
的直线交抛物线于![]() ,
,![]() 两点.
两点.
(1)求抛物线的方程;
(2)设直线![]() 是抛物线的准线,求证:以
是抛物线的准线,求证:以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抚州市某中学利用周末组织教职员工进行了一次秋季登军峰山健身的活动,有![]() 人参加,现将所有参加人员按年龄情况分为
人参加,现将所有参加人员按年龄情况分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等七组,其频率分布直方图如下图所示.已知
等七组,其频率分布直方图如下图所示.已知![]() 之间的参加者有4人.
之间的参加者有4人.
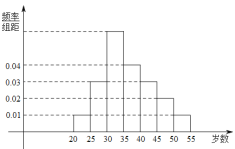
(1)求![]() 和
和![]() 之间的参加者人数
之间的参加者人数![]() ;
;
(2)组织者从![]() 之间的参加者(其中共有
之间的参加者(其中共有![]() 名女教师包括甲女,其余全为男教师)中随机选取
名女教师包括甲女,其余全为男教师)中随机选取![]() 名担任后勤保障工作,求在甲女必须入选的条件下,选出的女教师的人数为2人的概率.
名担任后勤保障工作,求在甲女必须入选的条件下,选出的女教师的人数为2人的概率.
(3)已知![]() 和
和![]() 之间各有
之间各有![]() 名数学教师,现从这两个组中各选取
名数学教师,现从这两个组中各选取![]() 人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有
人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有![]() 名数学教师的概率?
名数学教师的概率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com