
【题目】在极坐标系中,圆![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴正半轴建立直角坐标系
轴正半轴建立直角坐标系![]() ,直线
,直线![]() 经过点
经过点![]() 且倾斜角为
且倾斜角为![]() .
.
![]() 求圆
求圆![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的参数方程;
的参数方程;
![]() 已知直线
已知直线![]() 与圆
与圆![]() 交与
交与![]() ,
,![]() ,满足
,满足![]() 为
为![]() 的中点,求
的中点,求![]() .
.
科目:高中数学 来源: 题型:
【题目】(1)若点![]() 到直线
到直线![]() 的距离比它到点
的距离比它到点![]() 的距离小
的距离小![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
(2)设椭圆![]() 的离心率为
的离心率为![]() ,焦点在
,焦点在![]() 轴上且长轴长为
轴上且长轴长为![]() ,若曲线
,若曲线![]() 上的点到椭圆
上的点到椭圆![]() 的两个焦点的距离的差绝对值等于
的两个焦点的距离的差绝对值等于![]() ,求曲线
,求曲线![]() 的标准方程.
的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过底面是矩形的四棱锥FABCD的顶点F作EF∥AB,使AB=2EF,且平面ABFE⊥平面ABCD,若点G在CD上且满足DG=G![]() .
.

求证:(1)FG∥平面AED;
(2)平面DAF⊥平面BAF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是曲线
是曲线![]() 上的动点,点
上的动点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求直线![]() 及曲线
及曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与直线
与直线![]() 交于点
交于点![]() ,与曲线
,与曲线![]() 交于点
交于点![]() (与原点不重合),求
(与原点不重合),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近来国内一些互联网公司为了赢得更大的利润、提升员工的奋斗姿态,要求员工实行“996”工作制,即工作日早9点上班,晚上21点下班,中午和傍晚最多休息1小时,总计工作10小时以上,并且一周工作6天的工作制度,工作期间还不能请假,也没有任何补贴和加班费.消息一出,社交媒体一片哗然,有的人认为这是违反《劳动法》的一种对员工的压榨行为,有的人认为只有付出超越别人的努力和时间,才能够实现想要的成功,这是提升员工价值的一种有效方式.对此,国内某大型企业集团管理者认为应当在公司内部实行“996”工作制,但应该给予一定的加班补贴(单位:百元),对于每月的补贴数额集团人力资源管理部门随机抽取了集团内部的1000名员工进行了补贴数额(单位:百元)期望值的网上问卷调查,并把所得数据列成如下所示的频数分布表:
![]()
(1)求所得样本的中位数(精确到百元);
(2)根据样本数据,可近似地认为员工的加班补贴![]() 服从正态分布
服从正态分布![]() ,若该集团共有员工40000人,试估计有多少员工期待加班补贴在8100元以上;
,若该集团共有员工40000人,试估计有多少员工期待加班补贴在8100元以上;
(3)已知样本数据中期望补贴数额在![]() 范围内的8名员工中有5名男性,3名女性,现选其中3名员工进行消费调查,记选出的女职员人数为
范围内的8名员工中有5名男性,3名女性,现选其中3名员工进行消费调查,记选出的女职员人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
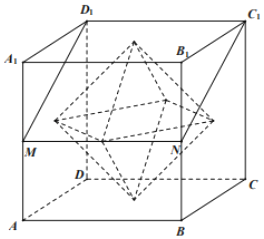
【题目】如图,点M,N分别为正方体ABCD﹣A1B1C1D1的棱AA1,BB1的中点,以正方体的六个面的中心为顶点构成一个八面体,若平面D1MNC1将该八面体分割成上、下两部分的体积分别为V1、V2,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com