
| A. | 4320 | B. | -4320 | C. | 20 | D. | -20 |
分析 先确定487被7除的余数为a,再利用$(x-\frac{6}{{x}^{2}})^{6}$展开式的通项,可得结论.
解答 解:487=(49-1)7=${C}_{7}^{0}•4{9}^{7}$-${C}_{7}^{1}•4{9}^{8}$+…+${C}_{7}^{6}•49$-1,
∵487被7除的余数为a(0≤a<7),
∴a=6,
∴$(x-\frac{6}{{x}^{2}})^{6}$展开式的通项为Tr+1=${C}_{6}^{r}•(-6)^{r}•{x}^{6-3r}$,
令6-3r=-3,可得r=3,
∴$(x-\frac{6}{{x}^{2}})^{6}$展开式中x-3的系数为${C}_{6}^{3}•(-6)^{3}$=-4320,
故选:B.
点评 本题考查二项式定理的运用,考查学生的计算能力,正确运用二项式定理是关键.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
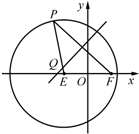 如图,已知圆E:${(x+\sqrt{3})^2}+{y^2}$=16,点$F(\sqrt{3},0)$,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:${(x+\sqrt{3})^2}+{y^2}$=16,点$F(\sqrt{3},0)$,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 已知p:?x0∈R,x02+x0-1=0,q:?x∈R,x2+x+1>0,则p∧q是真命题 | |
| B. | 命题p:若$\overrightarrow a⊥\overrightarrow b$,则$\overrightarrow a•\overrightarrow b=0$的否命题是:若$\overrightarrow a⊥\overrightarrow b$,则$\overrightarrow a•\overrightarrow b≠0$ | |
| C. | ?x∈R,x2+x-1<0的否定是?x0∈R,x02+x0-1>0 | |
| D. | x=$\frac{π}{3}$是$y=sin(2x-\frac{π}{6})$取最大值的充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m、n?α,m∥β,n∥β,则α∥β | B. | 若m?α,α∥β,则m∥β | ||
| C. | 若m⊥α,α⊥β,n∥β,则m⊥n | D. | 若α⊥γ,β⊥γ,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1) | B. | [0,1] | C. | (一∞,1) | D. | (一∞,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com