已知函数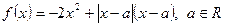
。
（I）当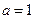
时，解不等式
；
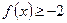（II）求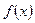
的最大值。
点睛新教材全能解读系列答案
小学教材完全解读系列答案科目：高中数学 来源： 题型：解答题
（本小题满分13分）
某工厂去年的某产品的年销售量为100万只，每只产品的销售价为10元，每只产品固定成本为8元．今年，工厂第一次投入100万元（科技成本），并计划以后每年比上一年多投入100万元（科技成本），预计销售量从今年开始每年比上一年增加10万只，第n次投入后，每只产品的固定成本为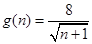
（
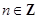且n≥0），若产品销售价保持不变，第n次投入后的年利润为
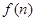万元．
（Ⅰ）求出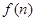的表达式；
（Ⅱ）若今年是第1年，问第几年年利润最高?最高利润为多少万元?
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)=|x-a|.
（Ⅰ）若不等式f(x)≥3的解集为{x|x≤1或x≥5}，求实数a的值；
（Ⅱ）在（Ⅰ）的条件下，若f(x)+f(x+4)≥m对一切实数x恒成立，求实数m的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本题满分14分）某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入1
00元，已知总收益满足函数：
，其中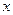
是仪器的月产量。
（1）将利润表示为月产量的函数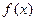
；
（2）当月产量为何值时，公司所获利润最大？最大利润为多少元？
（利润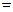
总收益
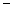总成本）
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
据预测，我国在“十二五”期间内某产品关税与市场供应量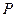
的关系近似地满足
：
（其中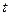
为关税的税率，且
，
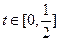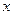为市场价格，
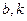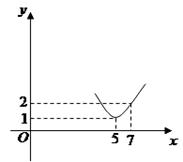
为正常数），当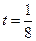
时的市场供应量曲线如图所示；
（1）根据图象求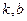
的值；
（2）若市场需求量为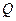
，它近似满足
.
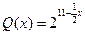当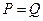
时的市场价格称为均衡价格，为使均衡价格控制在不低于9元的范围内，求税率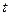的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
时，
，或
；
时，在
上
，
上
，
上最大值为
；
时，在
，
上
上最大值为
时，
时，
，
.
在
上存在零点，求实数
的取值范围；
时，若对任意的
，总存在
，使
，求实数
的取值范围．
且函数
的值域为
，求
的表达式；
为偶函数，判断
能否大于零？并说明理由。
；
，求
的值．