练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设△ABC的内角A，B，C所对的边分别为a，b，c，(a+b+c)(a－b+c)=ac

    (1)求B

    (2)若sinAsinC=，求C

     

    （1）120°

    （2）15°或45°

    【解析】（1）∵(a+b+c)(a－b+c)=ac

    ∴a2+c2－b2=－ac

    由余弦定理知cosB==－

    ∴B=120°

    （2）由（1）知A+C=60°

    ∵cos(A－C)=cosAcosC+sinAsinC

    = cosAcosC－sinAsinC+2sinAsinC

    =cos(A+C)+2sinAsinC

    =+=

    ∴A－C=30°或A－C=－30°，∴C=15°或C=45°

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014高考名师推荐数学理科利用导数求最值和极值（解析版） 题型：解答题

    已知函数．

    (1)设x=0是f(x)的极值点，求m，并讨论f(x)的单调性;

    (2)当m≤2时，证明f(x)>0．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科函数与方程（解析版） 题型：选择题

    若，则函数的两个零点分别位于区间( )

    A．(a，b)和(b，c)内

    B．(－∞，a)和(a，b)内

    C．(b，c)和(c，+∞)内 D．(－∞，a)和(c，+∞)内

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科几何概型（解析版） 题型：选择题

    如图，在矩形区域ABCD的A，C两点处各有一个通信基站，假设其信号的覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源，基站工作正常)．若在该矩形区域内随机地选一地点，则该地点无信号的概率是( )

    A． B． C． D．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科全称量词与存在性量词（解析版） 题型：选择题

    已知命题p：m<0，命题q：?x∈R，x2＋mx＋1>0成立，若“p∧q”为真命题，则实数m的取值范围是

    A.[－2，0]

    B.(0，2)

    C.(－2，0)

    D.(－2，2)

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科余弦定理（解析版） 题型：选择题

    某人要制作一个三角形，要求它的三条高的长度分别为，，，则此人能（    ）

    A．不能作出这样的三角形

    B．作出一个锐角三角形

    C．作出一个直角三角形

    D．作出一个钝角三角形

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科二项式定理与性质（解析版） 题型：选择题

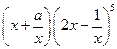    的展开式中各项系数的和为2，则该展开式中常数项为（ ）

    A．-40 B．-20 C．20 D．40

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科两角和与差的三角函数、倍角公式（解析版） 题型：选择题

    函数y=sin(+x)cos(-x)的最大值为（  ）

    A.

    B.

    C.

    D.

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科预测题（解析版） 题型：解答题

    某普通高中共有教师人，分为三个批次参加研修培训，在三个批次中男、女教师人数如下表所示：

     

    第一批次

    第二批次

    第三批次

    女教师

    男教师

     

    已知在全体教师中随机抽取1名，抽到第二、三批次中女教师的概率分别是、．

    （1）求的值；

    （2）为了调查研修效果，现从三个批次中按的比例抽取教师进行问卷调查，三个批次被选取的人数分别是多少？

    （3）若从（2）中选取的教师中随机选出两名教师进行访谈，求参加访谈的两名教师“分别来自两个批次”的概率．

     

    查看答案和解析>>

    同步练习册答案