
已知函数 .
.
(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(2)当m≤2时,证明f(x)>0.
(1)m=1(讨论见解析);
(2)见解析.
【解析】(1) .
.
由x=0是f(x)的极值点得f '(0)=0,所以m=1.
于是f(x)=ex-ln(x+1),定义域为(-1,+∞), .
.
函数 在(-1,+∞)上单调递增,且f '(0)=0,因此当x∈(-1,0)时, f '(x)<0;当x∈(0,+∞)时, f '(x)>0.
在(-1,+∞)上单调递增,且f '(0)=0,因此当x∈(-1,0)时, f '(x)<0;当x∈(0,+∞)时, f '(x)>0.
所以f(x)在(-1,0)上单调递减,在(0,+∞)上单调递增.
(2)当m≤2,x∈(-m,+∞)时,ln(x+m)≤ln(x+2),故只需证明当m=2时, f(x)>0.
当m=2时,函数 在(-2,+∞)上单调递增.
在(-2,+∞)上单调递增.
又f '(-1)<0, f '(0)>0,故f '(x)=0在(-2,+∞)上有唯一实根 ,且
,且 .
.
当 时, f '(x)<0;当
时, f '(x)<0;当 时, f '(x)>0,从而当
时, f '(x)>0,从而当 时,f(x)取得最小值.
时,f(x)取得最小值.
由f '(x0)=0得 =
= ,
,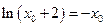 ,
,
故 .
.
综上,当m≤2时, f(x)>0.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源:2014高考名师推荐数学理科同角三角函数的基本关系式和诱导公式(解析版) 题型:选择题
已知tan =2,,则3sin2
=2,,则3sin2 -cos
-cos sin
sin +1= ( )
+1= ( )
A.3
B.-3
C.4
D.-4
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科双曲线(解析版) 题型:选择题
等轴双曲线 的中心在原点,焦点在
的中心在原点,焦点在 轴上,
轴上, 与抛物线
与抛物线 的准线交于
的准线交于 两点
两点 ,则
,则 的实轴长为( )
的实轴长为( )
A.
B.2
C.4
D.8
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科参数方程(解析版) 题型:解答题
在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系.已知点A的极坐标为( ,
, ),直线l的极坐标方程为ρcos(
),直线l的极坐标方程为ρcos(
 )=a,且点A在直线l上.
)=a,且点A在直线l上.
(1)求a的值及直线l的直角坐标方程;
(2)圆C的参数方程为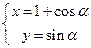 (
( 为参数),试判断直线l与圆C的位置关系.
为参数),试判断直线l与圆C的位置关系.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科余弦定理(解析版) 题型:解答题
设△ABC的内角A,B,C所对的边分别为a,b,c,(a+b+c)(a-b+c)=ac
(1)求B
(2)若sinAsinC= ,求C
,求C
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com