练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若四棱锥PABCD的底面是边长为2的正方形，PA⊥底面ABCD(如图)且PA＝2.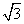

    (1)求异面直线PD与BC所成角的大小；

    (2)求四棱锥PABCD的体积．


    解析：(1)∵AD∥BC，∴∠PDA的大小即为异面直线PD与BC所成角的大小．

    ∵PA⊥平面ABCD，∴PA⊥AD，

    由PA＝2，AD＝2，得tan∠PDA＝，∴∠PDA＝60°，

    故异面直线PD与BC所成角的大小为60°.

    (2)∵PA⊥平面ABCD，

    ∴VP－ABCD＝S正方形ABCD·PA＝×22×2＝.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     “a≤0”是“函数在区间内单调递增”的（    ）

    A. 充分不必要条件       B. 必要不充分条件

    C. 充分必要条件         D. 既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线l，m，平面α，β，且l⊥α，m⊂β，则α∥β是l⊥m的(　　)

    A．充要条件

    B．充分不必要条件

    C．必要不充分条件

    D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示，已知一个半径为1的半球形容器①及容器②的三视图，侧视图矩形的宽为5，俯视图是边长为1的正三角形．

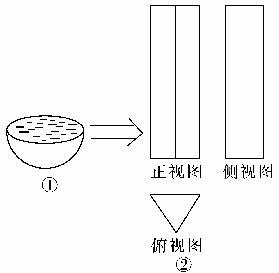
    (1)请画出容器②的直观图(简图，尺寸不作严格要求)，并回答：它是什么几何体？

    (2)若把容器①中盛满的水全部注入容器②中，水是否会从容器②中溢出？为什么？(参考数据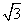：≈1.732)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    正方体ABCDA1B1C1D1中，E、F分别是线段BC、C1D的中点，则直线A1B与直线EF的位置关系是(　　)

    A．相交              B．平行

    C．异面              D．以上都有可能

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如下图，正方体ABCDA1B1C1D1中，E，F分别为棱AB，CC1的中点，在平面ADD1A1内且与平面D1EF平行的直线　(　　)

    A．不存在　               B．有1条

    C．有2条　               D．有无数条

    查看答案和解析>>

    科目：高中数学 来源： 题型：


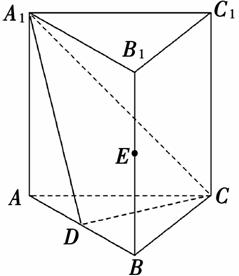
    如图，直三棱柱ABCA1B1C1中，D，E分别是AB，BB1的中点．

    (1)证明：BC1∥平面A1CD；

    (2)设AA1＝AC＝CB＝2，AB＝2，求三棱锥CA1DE的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    右图是函数y＝x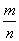 (m，n∈N*，m，n互质)的图象，则(　　)

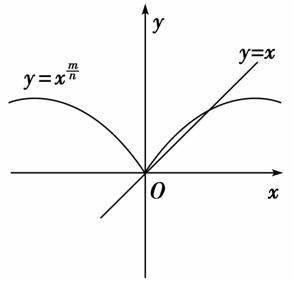
    A．m，n是奇数且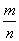＜1

    B．m是偶数，n是奇数且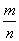＞1

    C．m是偶数，n是奇数且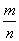＜1

    D．m是奇数，n是偶数且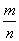＞1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝loga(x＋1)－loga(1－x)，a＞0且a≠1.

    (1)求f(x)的定义域；

    (2)判断f(x)的奇偶性并予以证明；

    (3)若a＞1时，求使f(x)＞0的x的解集．

    查看答案和解析>>

    同步练习册答案