
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |

| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
| P(K2≥x0) | 0.05 | 0.01 |
| x0 | 3.841 | 6.635 |
分析 (Ⅰ)利用所给数据,可得频率分布直方图,并比较女性用户和男性用户评分的波动大小;
(Ⅱ)由女性用户频率分布直方图知,女性用户评分的众数;在男性用户频率分布直方图中,中位数两边的面积相等,求出男性用户评分的中位数;
(Ⅲ)求出K2,与临界值比较,即可得出结论.
解答 解:(Ⅰ)女性用户和男性用户的频率分布表分别如下左、右图: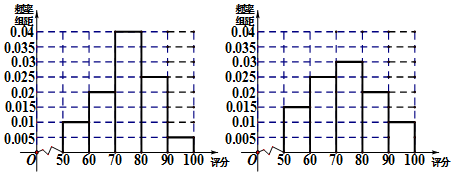
由图可得女性用户的波动小,男性用户的波动大. …(4分)
(Ⅱ)由女性用户频率分布直方图知,女性用户评分的众数为75; …(5分)
在男性用户频率分布直方图中,中位数两边的面积相等.设中位数为x,则70≤x<80
于是10×0.015+10×0.025+(x-70)×0.03=0.5,解得 $x=73\frac{1}{3}$…(8分)
(Ⅲ)2×2列联表如下图:
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
点评 本题考查频率分布直方图,考查独立性检验知识的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{7}$ | B. | 0 | C. | $\sqrt{7}$ | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\frac{{2-{x^2}}}{2x}$ | B. | f(x)=$\frac{cosx}{x^2}$ | C. | f(x)=$\frac{{{{cos}^2}x}}{x}$ | D. | f(x)=$\frac{cosx}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
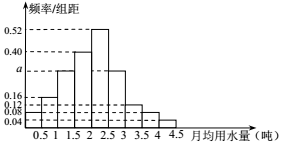 我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[1,\frac{7}{4}]$ | B. | $[-\frac{7}{4},-1]$ | C. | $[-\sqrt{2},-1]$ | D. | $[-1,\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{7}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com