已知函数f(x)=x2+lnx-ax.
(Ⅰ)当a=3时,求f(x)的单调增区间;
(Ⅱ)若f(x)在(0,1)上是增函数,求a得取值范围;
(Ⅲ)在(Ⅱ)的结论下,设g(x)=x2+|x-a|,(1≤x≤3),求函数g(x)的最小值.
解:(Ⅰ)当a=3时,f(x)=x
2+lnx-3x;
∴
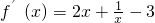
由f′(x)>0得,
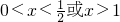
;
故所求f(x)的单调增区间为
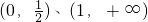
(Ⅱ)
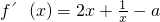
.
∵f(x)在(0,1)上是增函数,
∴
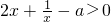
在(0,1)上恒成立,即
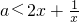
恒成立.
∵
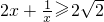
(当且仅当

时取等号).
所以
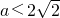
.
当
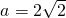
时,易知f(x)在(0,1)上也是增函数,
所以

.
(Ⅲ)由(Ⅱ)知

当a≤1时,g(x)=x
2+x-a在区间[1,3]上是增函数
所以g(x)的最小值为g(1)=2-a.
当

时,
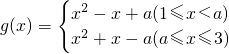
因为函数g(x)在区间[a,3]上是增函数,在区间[1,a]上也是增函数,
所以g(x)在[1,3]上为增函数,
所以g(x)的最小值为g(1)=a.
所以,当a≤1时,g(x)的最小值为2-a;
当

时,g(x)的最小值为a.
分析:(Ⅰ)求单调增区间,先求导,令导函数大于等于0即可.(Ⅱ)已知f(x)在区间(0,1)上是增函数,即f′(x)≥0在区间(0,1)上恒成立,然后用分离参数求最值即可.
(Ⅲ)去绝对值符号,转化为二次函数在定区间上求最值问题,对对称轴讨论.
点评:此题是难题.考查利用导数研究函数的单调性和二次函数在定区间上的最值问题,体现了分类讨论和转化的思想方法,考查了学生灵活应用知识分析解决问题的能力.

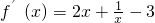
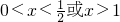 ;
;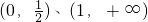
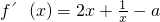 .
.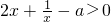 在(0,1)上恒成立,即
在(0,1)上恒成立,即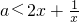 恒成立.
恒成立.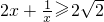 (当且仅当
(当且仅当 时取等号).
时取等号).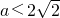 .
.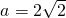 时,易知f(x)在(0,1)上也是增函数,
时,易知f(x)在(0,1)上也是增函数, .
. 
 时,
时,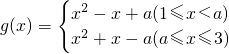
 时,g(x)的最小值为a.
时,g(x)的最小值为a.

 同步奥数系列答案
同步奥数系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<