
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
| 不满意 | 一般 | 比较满意 | 很好 |
| 1210 | 3998 | 2605 | 2187 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
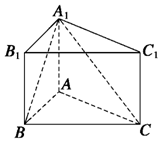 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅∉A | B. | $\sqrt{2}$∉A | C. | $\sqrt{2}∈A$ | D. | {$\sqrt{2}$}⊆A |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,菱形ABCD的边长为2,△BCD为正三角形,现将△BCD沿BD向上折起,折起后的点C记为C′,且CC′=$\sqrt{3}$,连接CC′,E为CC′的中点.
如图,菱形ABCD的边长为2,△BCD为正三角形,现将△BCD沿BD向上折起,折起后的点C记为C′,且CC′=$\sqrt{3}$,连接CC′,E为CC′的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米.
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com