
| A. | 960 | B. | 1240 | C. | 1320 | D. | 1440 |
分析 先分类,有2,2,1,1与3,1,1,1,两种情况,再用间接法,即可得出结论.
解答 解:根据题意,先分类,有2,2,1,1与3,1,1,1,两种情况,放法共有$\frac{{C}_{6}^{2}{C}_{4}^{2}{C}_{2}^{1}{C}_{1}^{1}}{{A}_{2}^{2}{A}_{2}^{2}}$•${A}_{4}^{4}$+$\frac{{C}_{6}^{3}{C}_{3}^{1}{C}_{2}^{1}{C}_{1}^{1}}{{A}_{3}^{3}}$•${A}_{4}^{4}$,
编号为3与6的卡片在同一个盒子中的不同放法共有$\frac{{C}_{5}^{2}{C}_{3}^{1}{C}_{2}^{1}{C}_{1}^{1}}{{A}_{3}^{3}}$•${A}_{4}^{4}$,
∴编号为3与6的卡片不在同一个盒子中的不同放法共有$\frac{C_6^2C_4^2C_2^1C_1^1}{A_2^2A_2^2}•A_4^4+\frac{C_6^3C_3^1C_2^1C_1^1}{A_3^3}•A_4^4-\frac{C_5^2C_3^1C_2^1C_1^1}{A_3^3}•A_4^4$=1320,
故选:C.
点评 本题考查计数原理的运用,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
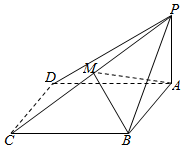 四棱锥P-ABCD中,底面ABCD为正方形,PA⊥面ABCD,PA=$\frac{1}{2}$AB.
四棱锥P-ABCD中,底面ABCD为正方形,PA⊥面ABCD,PA=$\frac{1}{2}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年份200x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数 y (十万) | 5 | 7 | 8 | t | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | [-1,1] | C. | [0,1] | D. | ∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com