
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由(1-2i)•z=i3,得$z=\frac{{i}^{3}}{1-2i}$,然后利用复数代数形式的乘除运算化简复数z,求出复数z在复平面内对应的点的坐标,则答案可求.
解答 解:由(1-2i)•z=i3,
得$z=\frac{{i}^{3}}{1-2i}$=$\frac{-i(1+2i)}{(1-2i)(1+2i)}=\frac{2-i}{5}=\frac{2}{5}-\frac{1}{5}i$,
则复数z在复平面内对应的点的坐标为:($\frac{2}{5}$,$-\frac{1}{5}$),位于第四象限.
故选:D.
点评 本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在三棱锥D-ABC,AB=BC=CD=DA=8,∠ADC=∠ABC=120°,M、O分别为棱BC,AC的中点,DM=4$\sqrt{2}$.
在三棱锥D-ABC,AB=BC=CD=DA=8,∠ADC=∠ABC=120°,M、O分别为棱BC,AC的中点,DM=4$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 960 | B. | 1240 | C. | 1320 | D. | 1440 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
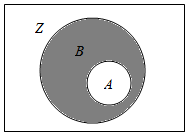 已知集合A={x∈Z|$\frac{x+1}{2-x}$≥0),B={x∈Z|-2<x≤3),则图中阴影部分表示的集合是( )
已知集合A={x∈Z|$\frac{x+1}{2-x}$≥0),B={x∈Z|-2<x≤3),则图中阴影部分表示的集合是( )| A. | {1,2,3) | B. | {2,3} | C. | {1,3} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某房地产公司的新建小区有A,B两种户型住宅,其中A户型住宅的每套面积为100平方米,B户型住宅的每套面积为80平方米.该公司准备从两种户型中各拿出10套试销售,如表是这20套住宅每平方米的销售价格(单位:万元/平方米).
某房地产公司的新建小区有A,B两种户型住宅,其中A户型住宅的每套面积为100平方米,B户型住宅的每套面积为80平方米.该公司准备从两种户型中各拿出10套试销售,如表是这20套住宅每平方米的销售价格(单位:万元/平方米).| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| A户型 | 0.7 | 1.3 | 1.1 | 1.4 | 1.1 | 0.9 | 0.8 | 0.8 | 1.3 | 0.9 |
| B户型 | 1.2 | 1.6 | 2.3 | 1.8 | 1.4 | 2.1 | 1.4 | 1.2 | 1.7 | 1.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4≤k≤1 | B. | -1≤k≤4 | C. | 1≤k≤4 | D. | k≥1或k≤-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com