Question

【题目】函数f（x）的定义域为D，若存在闭区间[a，b]D，使得函数f（x）满足：①f（x）在[a，b]内是单调函数；②f（x）在[a，b]上的值域为[2a，2b]，则称区间[a，b]为y=f（x）的“倍值区间”．下列函数中存在“倍值区间”的有（ ） ①f（x）=x2（x≥0）；
②f（x）=ex（x∈R）；
③f（x）= （x≥0）；
④f（x）= ．
A.①②③④
B.①②④
C.①③④
D.①③

Answer 1

【答案】C
【解析】解：函数中存在“倍值区间”，则：①f（x）在[a，b]内是单调函数；② 或 ①f（x）=x2（x≥0），若存在“倍值区间”[a，b]，则 ，∴ ∴
∴f（x）=x2（x≥0），若存在“倍值区间”[0，2]；
②f（x）=ex（x∈R），若存在“倍值区间”[a，b]，则 ，∴
构建函数g（x）=ex﹣2x，∴g′（x）=ex﹣2，
∴函数在（﹣∞，ln2）上单调减，在（ln2，+∞）上单调增，
∴函数在x=ln2处取得极小值，且为最小值．
∵g（ln2）=2﹣2ln2＞0，∴g（x）＞0恒成立，∴ex﹣2x=0无解，故函数不存在“倍值区间”；
③ ， =
若存在“倍值区间”[a，b][0，1]，则 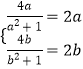，∴ ，∴a=0，b=1，若存在“倍值区间”[0，1]；
④ ．不妨设a＞1，则函数在定义域内为单调增函数
若存在“倍值区间”[m，n]，则 ，必有 ，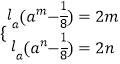
必有m，n是方程 的两个根，
必有m，n是方程 的两个根，
由于 存在两个不等式的根，故存在“倍值区间”[m，n]；
综上知，所给函数中存在“倍值区间”的有①③④
故选C．
【考点精析】解答此题的关键在于理解函数的定义域及其求法的相关知识，掌握求函数的定义域时，一般遵循以下原则：①是整式时，定义域是全体实数;②是分式函数时，定义域是使分母不为零的一切实数;③是偶次根式时，定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1,零（负）指数幂的底数不能为零，以及对函数的值域的理解，了解求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的．