
 ,乙获胜的概率为
,乙获胜的概率为 ,现已赛完两局,乙暂时以2∶0领先.
,现已赛完两局,乙暂时以2∶0领先.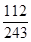 ;(2) X的概率分布为:
;(2) X的概率分布为:| X | 4 | 5 | 6 | 7 |
| P | ?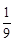 | ?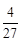 | ?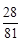 | ?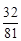 |
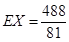 .
. ,由题意得随机变量
,由题意得随机变量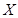 可能的取值为4,5,6,7,分别求出随机变量
可能的取值为4,5,6,7,分别求出随机变量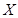 的概率,从而得分布列和数学期望.本题考查
的概率,从而得分布列和数学期望.本题考查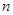 次独立重复试验中恰好发生
次独立重复试验中恰好发生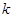 次的概率,解题的关键是正确理解两个事件、“甲获得这次比赛胜利”,再由概率的计算公式计算出概率.本题是概率中的有一定综合性的题,对事件正确理解与分类是很关键.
次的概率,解题的关键是正确理解两个事件、“甲获得这次比赛胜利”,再由概率的计算公式计算出概率.本题是概率中的有一定综合性的题,对事件正确理解与分类是很关键.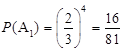 2分
2分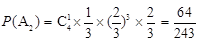 5分
5分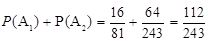 . 6分
. 6分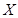 可能的取值为4,5,6,7,
可能的取值为4,5,6,7,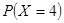 =
=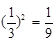 .
.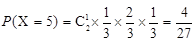 .
.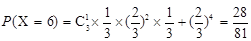 .
.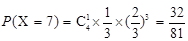 .
.| X | 4 | 5 | 6 | 7 |
| P | ?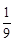 | ?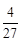 | ?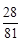 | ?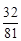 |
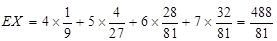 12分
12分

科目:高中数学 来源:不详 题型:解答题
 的社长是高中学生,
的社长是高中学生, 的社长是初中学生,高中社长中有
的社长是初中学生,高中社长中有 是高一学生,初中社长中有
是高一学生,初中社长中有 是初二学生.
是初二学生. ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
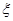 为取得红球的个数.
为取得红球的个数. 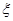 的分布列;
的分布列;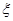 的数学期望
的数学期望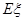 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
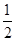 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是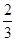 ,假设各局比赛结果相互独立.
,假设各局比赛结果相互独立.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,甲、丙二人都回答错的概率是
,甲、丙二人都回答错的概率是 ,乙、丙二人都回答对的概率是
,乙、丙二人都回答对的概率是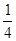 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com