
| A、(2,+∞) |
| B、[2,+∞) |
| C、[4,+∞) |
| D、(4,+∞) |
| 2e2x•2e-2x |
| 2 |
| t |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,正四棱锥S-ABCD的底面是边长为a的正方形,侧棱长是底面边长为
如图,正四棱锥S-ABCD的底面是边长为a的正方形,侧棱长是底面边长为| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| 2 |
| an |
| an+1 |
| an+1 |
| an |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
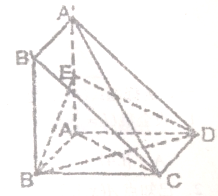 四边形ABCD与A′ABB′都是边长为a的正方形,且平面ABB′A′⊥平面ABCD,点E是A′A的中心.
四边形ABCD与A′ABB′都是边长为a的正方形,且平面ABB′A′⊥平面ABCD,点E是A′A的中心.查看答案和解析>>
科目:高中数学 来源: 题型:
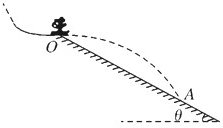 如图,跳台滑雪运动员(可视为质点)经过一段加速滑行后从O点水平飞出,落到斜坡上的A点,已知O点是斜坡的起点,测得A点与O点距离L=12m,斜坡与水平的夹角θ=37°,运动员的质量m=50kg,不计空气阻力,取sin37°=0.60,cos37°=0.80,g取10m/s2.求:
如图,跳台滑雪运动员(可视为质点)经过一段加速滑行后从O点水平飞出,落到斜坡上的A点,已知O点是斜坡的起点,测得A点与O点距离L=12m,斜坡与水平的夹角θ=37°,运动员的质量m=50kg,不计空气阻力,取sin37°=0.60,cos37°=0.80,g取10m/s2.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com