
【题目】已知函数![]() (
(![]() ,
, ![]() 是自然对数的底数).
是自然对数的底数).
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由导数几何意义得切线斜率为![]() ,再根据点斜式求切线方程(2)不等式恒成立问题,一般转化为对应函数最值问题:
,再根据点斜式求切线方程(2)不等式恒成立问题,一般转化为对应函数最值问题: ![]() ,利用导数研究函数
,利用导数研究函数![]() 最小值时,先根据
最小值时,先根据![]() ,得导函数在
,得导函数在![]() 上单调递增,因此
上单调递增,因此![]() ,即得实数
,即得实数![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)当![]() 时,有
时,有![]() ,
,
则![]() .
.
又因为![]() ,
,
∴曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]()
(Ⅱ)因为![]() ,令
,令![]()
有![]() (
(![]() )且函数
)且函数![]() 在
在![]() 上单调递增
上单调递增
当![]() 时,有
时,有![]() ,此时函数
,此时函数![]() 在
在![]() 上单调递增,则
上单调递增,则![]()
(ⅰ)若![]() 即
即![]() 时,有函数
时,有函数![]() 在
在![]() 上单调递增,
上单调递增,
则![]() 恒成立;
恒成立;
(ⅱ)若![]() 即
即![]() 时,则在
时,则在![]() 存在
存在![]() ,
,
此时函数![]() 在
在![]() 上单调递减,
上单调递减, ![]() 上单调递增且
上单调递增且![]() ,
,
所以不等式不可能恒成立,故不符合题意;
当![]() 时,有
时,有![]() ,则在
,则在![]() 存在
存在![]() ,此时
,此时![]() 上单调递减,
上单调递减, ![]() 上单调递增所以函数
上单调递增所以函数![]() 在
在![]() 上先减后增.
上先减后增.
又![]() ,则函数
,则函数![]() 在
在![]() 上先减后增且
上先减后增且![]() .
.
所以不等式不可能恒成立,故不符合题意;
综上所述,实数![]() 的取值范围为
的取值范围为![]()


科目:高中数学 来源: 题型:
【题目】设函数f(x)=lg[log ![]() (
( ![]() x﹣1)]的定义域为集合A,集合B={x|x<1,或x≥3}.
x﹣1)]的定义域为集合A,集合B={x|x<1,或x≥3}.
(1)求A∪B,(RB)∩A;
(2)若2a∈A,且log2(2a﹣1)∈B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名运动员参加“选拔测试赛”,在相同条件下,两人6次测试的成绩(单位:分)记录如下:
甲 86 77 92 72 78 84
乙 78 82 88 82 95 90
(1)用茎叶图表示这两组数据,现要从中选派一名运动员参加比赛,你认为选派谁参赛更好?说明理由(不用计算);
(2)若将频率视为概率,对运动员甲在今后三次测试成绩进行预测,记这三次成绩高于85分的次数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() 及方差
及方差![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等比数列,a1=1,a4=27; Sn为等差数列{bn} 的前n 项和,b1=3,S5=35.
(1)求{an}和{bn} 的通项公式;
(2)设数列{cn} 满足cn=anbn(n∈N*),求数列{cn} 的前n 项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线C1:  ( t 为参数),曲线C2:
( t 为参数),曲线C2: ![]() (r>0,θ为参数).
(r>0,θ为参数).
(1)当r=1时,求C 1 与C2的交点坐标;
(2)点P 为曲线 C2上一动点,当r=![]() 时,求点P 到直线C1距离最大时点P 的坐标.
时,求点P 到直线C1距离最大时点P 的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
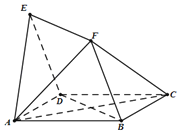
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求证:FC∥平面EAD;
(Ⅲ)求二面角A﹣FC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (t为参数),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=﹣
(t为参数),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=﹣ ![]() .
.
(1)求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)若C1上的点P对应的参数为t= ![]() ,Q为C2上的动点,求PQ中点M到直线C3:
,Q为C2上的动点,求PQ中点M到直线C3: ![]() (α为参数)距离的最小值.
(α为参数)距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com