
【题目】设函数f(x)=lg[log ![]() (
( ![]() x﹣1)]的定义域为集合A,集合B={x|x<1,或x≥3}.
x﹣1)]的定义域为集合A,集合B={x|x<1,或x≥3}.
(1)求A∪B,(RB)∩A;
(2)若2a∈A,且log2(2a﹣1)∈B,求实数a的取值范围.
【答案】
(1)解:函数f(x)=lg[log ![]() (
( ![]() x﹣1)]的定义域是集合A;
x﹣1)]的定义域是集合A;
函数f(x)的定义域满足. ![]() ,
,
∴ ![]() ,
,
∴2<x<4,
∴集合A=(2,4);
集合B={x|x<1,或x≥3}.即B=(﹣∞,1)∪[3,+∞),
∴RB=[1,3),
故得∴A∪B=(﹣∞,1)∪(2,+∞);
(RB)∩A=(2,3)
(2)解:由(1)得A=(2,4);B=(﹣∞,1)∪[3,+∞),
∵2a∈A,
∴2<2a<4,
解得:1<a<2,
又∵log2(2a﹣1)∈B,
∴log2(2a﹣1)<1或log2(2a﹣1)≥3,
∴0<2a﹣1<2或2a﹣1≥8,
解得 ![]()
∴ ![]() .
.
所以实数a的取值范围是(1, ![]() )
)
【解析】(1)由题意:求函数的定义域得到集合A,在根据集合的基本运算求解A∪B,(RB)∩A;(2)因为2a∈A,log2(2a﹣1)∈B,即A是2a的值域,B是log2(2a﹣1)的值域,即可求解a的范围.
【考点精析】本题主要考查了元素与集合关系的判断和对数的运算性质的相关知识点,需要掌握对象![]() 与集合
与集合![]() 的关系是
的关系是![]() ,或者
,或者![]() ,两者必居其一;①加法:
,两者必居其一;①加法:![]() ②减法:
②减法:![]() ③数乘:
③数乘:![]() ④
④![]() ⑤
⑤![]() 才能正确解答此题.
才能正确解答此题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】如图,椭圆![]()
![]() 过点
过点![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,离心率
,离心率![]() ,
, ![]() 是椭圆右准线上的两个动点,且
是椭圆右准线上的两个动点,且![]() .
.
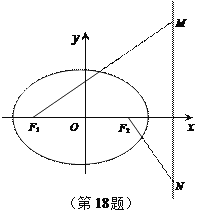
(1)求椭圆的方程;
(2)求![]() 的最小值;
的最小值;
(3)以![]() 为直径的圆
为直径的圆![]() 是否过定点?请证明你的结论.
是否过定点?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(1﹣x)+loga(x+3),(0<a<1).
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣2,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如表的列联表.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 100 |
已知在全部100人中抽到随机抽取1人为优秀的概率为 ![]()
(1)请完成如表的列联表;
(2)根据列联表的数据,有多大的把握认为“成绩与班级有关系“?
(3)按分层抽样的方法,从优秀学生中抽出6名学生组成一个样本,再从样本中抽出2名学生,记甲班被抽到的人数为ξ,求ξ的分布列和数学期望.
参考公式和数据:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
下面的临界值表供参考:
p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(0,﹣4),且倾斜角为 ![]() ,圆C的极坐标方程为ρ=4cosθ.
,圆C的极坐标方程为ρ=4cosθ.
(1)求直线l的参数方程和圆C的直角坐标方程;
(2)若直线l和圆C相交于A、B两点,求|PA||PB|及弦长|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2+bx+c(b,c∈R,b<0).
(1)若f(x)的定义域为[0,1]时,值域也是[0,1],求b,c的值;
(2)若b=﹣2时,若函数g(x)= ![]() 对任意x∈[3,5],g(x)>c恒成立,试求实数c的取值范围.
对任意x∈[3,5],g(x)>c恒成立,试求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下:

若以上表中频率作为概率,且每天的销售量相互独立.
(1)求5天中该种商品恰好有两天的日销售量为1.5吨的概率;
(2)已知每吨该商品的销售利润为2千元, ![]() 表示该种商品某两天销售利润的和(单位:千元),求
表示该种商品某两天销售利润的和(单位:千元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com