
 ,证明数列{an}成等比数列,并求数列{xn}的通项公式.
,证明数列{an}成等比数列,并求数列{xn}的通项公式. (2)见解析(3)xn=
(2)见解析(3)xn=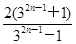
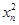 -4)=2xn(x-xn).
-4)=2xn(x-xn).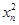 -4)=2xn(xn+1-xn).
-4)=2xn(xn+1-xn).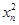 +4=2xnxn+1.显然xn≠0,∴xn+1=
+4=2xnxn+1.显然xn≠0,∴xn+1= .
. ≤x1,∴
≤x1,∴ ≥4.而x1>0,即有x1≥2.
≥4.而x1>0,即有x1≥2. ,
, ≥2
≥2 =2(n≥1),
=2(n≥1), -xn=
-xn=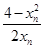 =
= ≤0.?
≤0.? ,知xn+1+2=
,知xn+1+2= ,
, .故
.故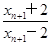 =(
=( )2.
)2. 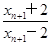 =2lg
=2lg ,即an+1=2an.所以,数列{an}成等比数列,
,即an+1=2an.所以,数列{an}成等比数列, =2n-1lg 3,
=2n-1lg 3, =2n-1lg 3.从而
=2n-1lg 3.从而 =32n-1,所以xn=
=32n-1,所以xn=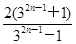 .
.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源:不详 题型:解答题
 时,该商品的价格上涨多少,才能使销售的总金额达到最大?
时,该商品的价格上涨多少,才能使销售的总金额达到最大?查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.ex+1 | B.ex-1 |
| C.e-x+1 | D.e-x-1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.P点 | B.Q点 | C.R点 | D.S点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com