
(本小题满分12分)已知函数 ,
,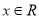 .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)在 中,角
中,角 所对的边分别是
所对的边分别是 ,若
,若 ,
,
 ,试求
,试求 的面积.
的面积.
(Ⅰ)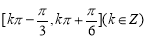 (Ⅱ)
(Ⅱ)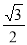 .
.
【解析】
试题分析:(Ⅰ)单调性:根据y=sint和t=ωx+φ的单调性来研究,由-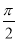 +2kπ≤ωx+φ≤
+2kπ≤ωx+φ≤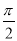 +2kπ,k∈Z得单调增区间;由
+2kπ,k∈Z得单调增区间;由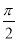 +2kπ≤ωx+φ≤
+2kπ≤ωx+φ≤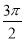 +2kπ,k∈Z得单调减区间.(Ⅱ)在解决三角形问题中,面积公式S=
+2kπ,k∈Z得单调减区间.(Ⅱ)在解决三角形问题中,面积公式S=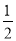 absinC=
absinC=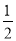 bcsinA=
bcsinA=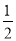 acsinB最常用,公式中既有边也有角,容易和正弦定理、余弦定理结合应用.在解面积与正、余弦定理结合的题目时,要注意整体代换方法的运用,如面积公式中含ab时可在余弦定理中通过变形得出a+b的形式.
acsinB最常用,公式中既有边也有角,容易和正弦定理、余弦定理结合应用.在解面积与正、余弦定理结合的题目时,要注意整体代换方法的运用,如面积公式中含ab时可在余弦定理中通过变形得出a+b的形式.
试题解析:
(Ⅰ)
∵ 4分
4分
由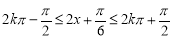 得:
得: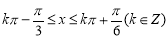
因此,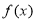 的单调递增区间是
的单调递增区间是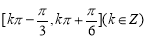 6分
6分
(Ⅱ)由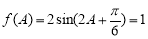 得:
得: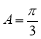 , 8分
, 8分
由余弦定理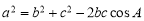 得:
得: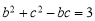 ①
①
由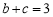 得:
得: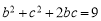 ② 10分
② 10分
②-①得: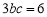 ,
,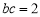
∴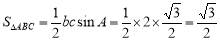 . 12分
. 12分
考点:三角函数、解三角形.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源:2014-2015学年广东省高一上学期阶段一考试数学试卷(解析版) 题型:选择题
已知函数f (x)的定义域是 [ 0 , 2 ] , 则函数y = f (x+1)+f (2x-1)的定义域是( )
A [-1 , 1] B [, 1 ] C [,] D [ 0 , ]
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省高一上学期期初考试数学试卷(解析版) 题型:选择题
已知f(x)为R上的减函数,则满足f(2x-1)<f(1)的实数x的取值范围是( )
A.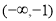 B.
B.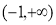 C.
C.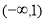 D.
D.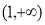
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山西省校高一上学期第一次考试数学试卷(解析版) 题型:选择题
若函数y=x2+(2a-1)x+1在区间(-∞,2 上是减函数,则实数a的取值范围是( )
上是减函数,则实数a的取值范围是( )
A. -
- ,+∞) B.(-∞,-
,+∞) B.(-∞,-
 C.
C.
 ,+∞) D.(-∞,
,+∞) D.(-∞,

查看答案和解析>>
科目:高中数学 来源:2014-2015学年山西省等校高二上学期期中联考文科数学试卷(解析版) 题型:选择题
如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在
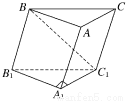
A.直线AB上 B.直线BC上
C.直线AC上 D.△ABC内部
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊三县市高二上学期联考数学试卷(解析版) 题型:选择题
已知△ABC三边满足a2+b2=c2- ab,则此三角形的最大内角为________.
ab,则此三角形的最大内角为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com