
根据我国汽车制造的现实情况,一般卡车高3 m,宽1.6 m.现要设计横断面为抛物线型的双向二车道的公路隧道,为保障双向行驶安全,交通管理规定汽车进入隧道后必须保持距中线0.4 m的距离行驶.已知拱口AB宽恰好是拱高OC的4倍,若拱宽为a m,求能使卡车安全通过的a的最小整数值.
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:解答题
设双曲线 的两个焦点分别为
的两个焦点分别为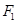 、
、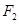 ,离心率为2.
,离心率为2.
(1)求双曲线的渐近线方程;
(2)过点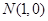 能否作出直线
能否作出直线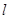 ,使
,使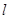 与双曲线
与双曲线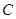 交于
交于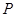 、
、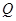 两点,且
两点,且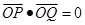 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知中心在原点的双曲线C的右焦点为(2,0),实轴长为2.
(1)求双曲线C的方程;
(2)若直线l:y=kx+与双曲线C左支交于A、B两点,求k的取值范围;
(3)在(2)的条件下,线段AB的垂直平分线l0与y轴交于M(0,m),求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)在平面直角坐标系中,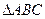 的两个顶点
的两个顶点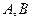 的坐标分别为
的坐标分别为 ,平面内两点
,平面内两点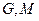 同时满足一下条件:①
同时满足一下条件:①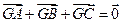 ;②
;②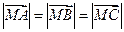 ;③
;③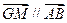
(1)求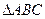 的顶点
的顶点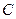 的轨迹方程;
的轨迹方程;
(2)过点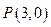 的直线
的直线 与(1)中的轨迹交于
与(1)中的轨迹交于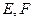 两点,求
两点,求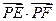 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在极坐标系中,圆ρ=2cos θ的垂直于极轴的两条切线方程分别为( )
| A.θ=0(ρ∈R)和ρcos θ=2 | B.θ=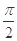 (ρ∈R)和ρcos θ=2 (ρ∈R)和ρcos θ=2 |
C.θ=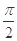 (ρ∈R)和ρcos θ=1 (ρ∈R)和ρcos θ=1 | D.θ=0(ρ∈R)和ρcos θ=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com