
设双曲线 的两个焦点分别为
的两个焦点分别为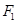 、
、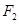 ,离心率为2.
,离心率为2.
(1)求双曲线的渐近线方程;
(2)过点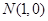 能否作出直线
能否作出直线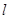 ,使
,使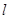 与双曲线
与双曲线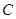 交于
交于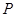 、
、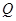 两点,且
两点,且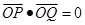 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
(本题满分12分)
如图,已知椭圆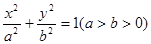 的长轴为
的长轴为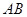 ,过点
,过点 的直线
的直线 与
与 轴垂直,直线
轴垂直,直线 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率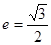

(1)求椭圆的标准方程;
(2)设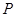 是椭圆上异于
是椭圆上异于 、
、 的任意一点,
的任意一点, 轴,
轴,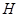 为垂足,延长
为垂足,延长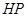 到点
到点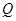 使得
使得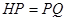 ,连接
,连接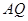 并延长交直线
并延长交直线 于点
于点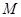 ,
,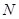 为
为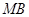 的中点.试判断直线
的中点.试判断直线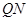 与以
与以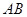 为直径的圆
为直径的圆 的位置关系.
的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)如图,已知椭圆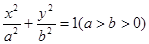 的离心率为
的离心率为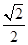 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点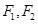 为顶点的三角形的周长为
为顶点的三角形的周长为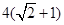 .一等轴双曲线的顶点是该椭圆的焦点,设
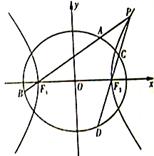
.一等轴双曲线的顶点是该椭圆的焦点,设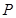 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线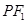 和
和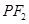 与椭圆的交点分别为
与椭圆的交点分别为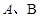 和
和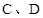 .
.
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线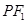 、
、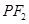 的斜率分别为
的斜率分别为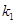 、
、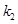 ,证明
,证明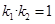 ;
;
(Ⅲ)是否存在常数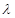 ,使得
,使得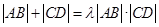 恒成立?若存在,求
恒成立?若存在,求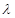 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)离心率为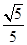 的椭圆
的椭圆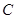 :
: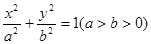 的左、右焦点分别为
的左、右焦点分别为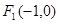 、
、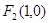 ,
,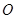 是坐标原点.
是坐标原点.
(1)求椭圆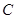 的方程;
的方程;
(2)若直线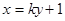 与
与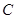 交于相异两点
交于相异两点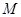 、
、 ,且
,且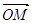

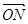
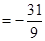 ,求
,求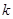 .(其中
.(其中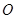 是坐标原点)
是坐标原点)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在直角坐标系 中,点P到两定点
中,点P到两定点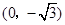 ,
,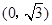 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为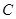 ,过点
,过点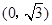 的直线C交于A,B两点.
的直线C交于A,B两点.
(1)写出C的方程;
(2)设d为A、B两点间的距离,d是否存在最大值、最小值,若存在, 求出d的最大值、最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在平面直角坐标系 中,
中, 是抛物线
是抛物线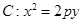
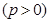 的焦点,
的焦点,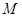 是抛物线
是抛物线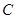 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过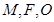 三点的圆的圆心为
三点的圆的圆心为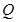 ,点
,点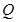 到抛物线
到抛物线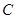 的准线的距离为
的准线的距离为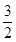 .(Ⅰ)求抛物线
.(Ⅰ)求抛物线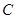 的方程;(Ⅱ)是否存在点
的方程;(Ⅱ)是否存在点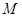 ,使得直线
,使得直线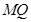 与抛物线
与抛物线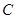 相切于点
相切于点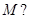 若存在,求出点
若存在,求出点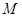 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
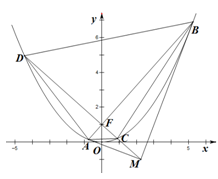
已知抛物线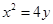 的焦点为
的焦点为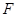 ,过焦点
,过焦点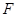 且不平行于
且不平行于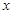 轴的动直线
轴的动直线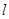 交抛物线于
交抛物线于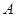 ,
,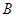 两点,抛物线在
两点,抛物线在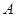 、
、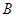 两点处的切线交于点
两点处的切线交于点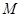 .
.

(Ⅰ)求证: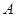 ,
,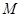 ,
,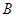 三点的横坐标成等差数列;
三点的横坐标成等差数列;
(Ⅱ)设直线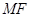 交该抛物线于
交该抛物线于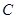 ,
, 两点,求四边形
两点,求四边形 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
根据我国汽车制造的现实情况,一般卡车高3 m,宽1.6 m.现要设计横断面为抛物线型的双向二车道的公路隧道,为保障双向行驶安全,交通管理规定汽车进入隧道后必须保持距中线0.4 m的距离行驶.已知拱口AB宽恰好是拱高OC的4倍,若拱宽为a m,求能使卡车安全通过的a的最小整数值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com