练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如果椭圆的对称轴为坐标轴，短轴的一个端点与两焦点组成一正三角形，焦点在y轴上，且a﹣c=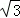那么椭圆的方程是　 　．

     

    【解析】

    试题分析：根据短轴的一个端点与两焦点组成一正三角形，焦点在y轴上知在结合a﹣c=与a2=b2+c2求出a，b，c即可

    【解析】
    由题意可设椭圆方程为：

    ∵短轴的一个端点与两焦点组成一正三角形，焦点在y轴上

    ∴

    又∵a﹣c=，a2=b2+c2

    ∴a2=12，b2=9

    ∴椭圆的方程为：

    故答案为：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年苏教版选修1-2 3.2复数的四则运算练习卷（解析版） 题型：选择题

    复数=（ ）

    A.1+2i B.1﹣2i C.﹣1 D.3

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-1 3.4导数在实际生活中的应用练习卷（解析版） 题型：填空题

    已知某生产厂家的年利润y（单位：万元）与年产量x（单位：万件）函数关系式为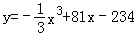，则使该生产厂家获取最大年利润的年产量为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-1 3.2导数的运算练习卷（解析版） 题型：填空题

    曲线y=x3在点（0，0）处的切线方程是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-1 2.5圆锥曲线与方程练习卷（解析版） 题型：解答题

    已知椭圆的两焦点为F1（0，﹣1）、F2（0，1），直线y=4是椭圆的一条准线．

    （1）求椭圆方程；

    （2）设点P在椭圆上，且|PF1|﹣|PF2|=1，求tan∠F1PF2的值．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-1 2.5圆锥曲线与方程练习卷（解析版） 题型：选择题

    若抛物线顶点为（0，0），对称轴为x轴，焦点在3x﹣4y﹣12=0上那么抛物线的方程为（　　）

    A.y2=16x B.y2=﹣16x C.y2=12x D.y2=﹣12x

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-1 2.4抛物线练习卷（解析版） 题型：解答题

    已知抛物线x2=4y，点P是抛物线上的动点，点A的坐标为（12，6），求点P到点A的距离与到x轴的距离之和的最小值．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-1 2.1圆锥曲线练习卷（解析版） 题型：解答题

    已知定点，F是椭圆的右焦点，在椭圆上求一点M，使|AM|+2|MF|取得最小值．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-1 1.2简单的逻辑联结词练习卷（解析版） 题型：填空题

    已知命题p1：函数y=2x﹣2﹣x在R上为增函数，p2：函数y=2x+2﹣x在R上为减函数，则在命题q1：p1或p2；q2：p1且p2；q3：（￢p1）或p2；q4：p1且（￢p2）中，真命题有 ．

     

    查看答案和解析>>

    同步练习册答案