
【题目】某校某班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生有14人.

(1)求总人数N和分数在120~125的人数n;
(2)利用频率分布直方图,估算该班学生数学成绩的众数和中位数各是多少?
科目:高中数学 来源: 题型:
【题目】(2017·衢州调研)已知四棱锥P-ABCD的底面ABCD是菱形,∠ADC=120°,AD的中点M是顶点P在底面ABCD的射影,N是PC的中点.

(1)求证:平面MPB⊥平面PBC;
(2)若MP=MC,求直线BN与平面PMC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过去大多数人采用储蓄的方式将钱储蓄起来,以保证自己生活的稳定![]() 考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式
考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式![]() 随着金融业的发展,普通人能够使用的投资理财工具也多了起来
随着金融业的发展,普通人能够使用的投资理财工具也多了起来![]() 为了研究某种理财工具的使用情况,现对
为了研究某种理财工具的使用情况,现对![]() 年龄段的人员进行了调查研究,将各年龄段人数分成5组:
年龄段的人员进行了调查研究,将各年龄段人数分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并整理得到频率分布直方图:
,并整理得到频率分布直方图:
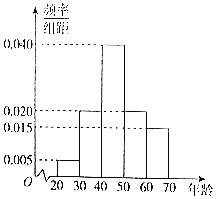
![]() Ⅰ
Ⅰ![]() 估计使用这种理财工具的人员年龄的中位数、平均数;
估计使用这种理财工具的人员年龄的中位数、平均数;
![]() Ⅱ
Ⅱ![]() 采用分层抽样的方法,从第二组、第三组、第四组中共抽取8人,则三个组中各抽取多少人?
采用分层抽样的方法,从第二组、第三组、第四组中共抽取8人,则三个组中各抽取多少人?
![]() Ⅲ
Ⅲ![]() 在
在![]() Ⅱ
Ⅱ![]() 中抽取的8人中,随机抽取2人,则第三组至少有1个人被抽到的概率是多少?
中抽取的8人中,随机抽取2人,则第三组至少有1个人被抽到的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:平面内到两个定点![]() 的距离之比为定值
的距离之比为定值![]() 的点所形成的图形是圆.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.已知在平面直角坐标系
的点所形成的图形是圆.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.已知在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,点
,点![]() 满足
满足![]() .设点
.设点![]() 所构成的曲线为
所构成的曲线为![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.![]() 的方程为
的方程为![]()
B.在![]() 上存在点
上存在点![]() ,使得
,使得![]() 到点
到点![]() 的距离为
的距离为![]()
C.在![]() 上存在点
上存在点![]() ,使得
,使得![]()
D.在![]() 上存在点
上存在点![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“伦敦眼”坐落在英国伦敦泰晤士河畔,是世界上首座观景摩天轮,又称“千禧之轮”,该摩天轮的半径为6(单位:![]() ),游客在乘坐舱
),游客在乘坐舱![]() 升到上半空鸟瞰伦敦建筑
升到上半空鸟瞰伦敦建筑![]() ,伦敦眼与建筑之间的距离
,伦敦眼与建筑之间的距离![]() 为12(单位:
为12(单位:![]() ),游客在乘坐舱
),游客在乘坐舱![]() 看建筑
看建筑![]() 的视角为
的视角为![]() .
.

(1)当乘坐舱![]() 在伦敦眼的最高点
在伦敦眼的最高点![]() 时,视角
时,视角![]() ,求建筑
,求建筑![]() 的高度;
的高度;
(2)当游客在乘坐舱![]() 看建筑
看建筑![]() 的视角
的视角![]() 为
为![]() 时,拍摄效果最好.若在伦敦眼上可以拍摄到效果最好的照片,求建筑
时,拍摄效果最好.若在伦敦眼上可以拍摄到效果最好的照片,求建筑![]() 的最低高度.
的最低高度.
(说明:为了便于计算,数据与实际距离有误差,伦敦眼的实际高度为![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 中,角A,B,C的对边为a,b,c,现给出以下四个命题:
中,角A,B,C的对边为a,b,c,现给出以下四个命题:
![]() 当
当![]() ,
,![]() ,
,![]() 时,满足条件的三角形共有1个;
时,满足条件的三角形共有1个;
![]() 若三角形a:b:
若三角形a:b:![]() :5:7,这个三角形的最大角是
:5:7,这个三角形的最大角是![]() ;
;
![]() 如果
如果![]() ,那么
,那么![]() 的形状是直角三角形;
的形状是直角三角形;
![]() 若
若![]() ,
,![]() ,
,![]() ,则
,则![]() 在
在![]() 方向的投影为
方向的投影为![]() .
.
以上命题中所有正确命题的序号是______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com