练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中， ，则的最大值为__________

    【答案】

    【解析】∵acosB﹣bcosA=c，

    ∴结合正弦定理，得sinAcosB﹣sinBcosA=sinC，

    ∵C=π﹣（A+B），得sinC=sin（A+B）

    ∴sinAcosB﹣sinBcosA=（sinAcosB+cosAsinB）

    整理，得sinAcosB=4sinBcosA，同除以cosAcosB，得tanA=4tanB

    由此可得tan（A﹣B）=

    ∵A、B是三角形内角，且tanA与tanB同号

    ∴A、B都是锐角，即tanA＞0，tanB＞0

    ∵+4tanB≥4

    ∴tan（A﹣B）=≤，当且仅当=4tanB，即tanB=时，tan（A﹣B）的最大值为.

    故答案为： .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某校某班在一次数学测验中，全班N名学生的数学成绩的频率分布直方图如下，已知分数在110～120的学生有14人.

    (1)求总人数N和分数在120～125的人数n；

    (2)利用频率分布直方图，估算该班学生数学成绩的众数和中位数各是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】摩拜单车和小黄车等各种共享单车的普及给我们的生活带来了便利.已知某共享单车的收费标准是:每车使用不超过1小时（包含1小时）是免费的,超过1小时的部分每小时收费1元（不足1小时的部分按1小时计算,例如:骑行2.5小时收费2元）.现有甲、乙两人各自使用该种共享单车一次.设甲、乙不超过1小时还车的概率分别为1小时以上且不超过2小时还车的概率分别为两人用车时间都不会超过3小时.

    （Ⅰ）求甲乙两人所付的车费相同的概率;

    （Ⅱ）设甲乙两人所付的车费之和为随机变量求的分布列及数学期望

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解学生的身体状况，某校随机抽取了一批学生测量体重．经统计，这批学生的体重数据（单位：千克）全部介于到之间，将数据分成以下组：第组，第组，第组，第组，第组，得到如图所示的频率分布直方图，现采用分层抽样的方法，从第， ， 组中随机抽取名学生做初检．

    （）求每组抽取的学生人数．

    （）若从名学生中再次随机抽取名学生进行复检，求这名学生不在同一组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直角梯形中， ， ， 平面， ， ， 的中点为．

    （）求证： 面．

    （）求证：平面平面．

    （）当为何值时，能使？请给出证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室，地面形状如图所示，已知已有两面墙的夹角为，墙的长度为米，（已有两面墙的可利用长度足够大），记.

    （1）若，求的周长（结果精确到0.01米）；

    （2）为了使小动物能健康成长，要求所建的三角形露天活动室面积，的面积尽可能大，当为何值时，该活动室面积最大？并求出最大面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设是由一平面内的个向量组成的集合．若，且的模不小于中除外的所有向量和的模．则称是的极大向量.有下列命题：

    ①若中每个向量的方向都相同，则中必存在一个极大向量；

    ②给定平面内两个不共线向量，在该平面内总存在唯一的平面向量，使得中的每个元素都是极大向量；

    ③若中的每个元素都是极大向量，且中无公共元素，则中的每一个元素也都是极大向量．

    其中真命题的序号是_______________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是某单位职工的月收入情况画出的样本频率分布直方图，已知图中第一组的频数为4 000，请根据该图提供的信息，解答下列问题．

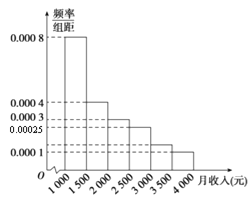
    (1)为了分析职工的收入与年龄、学历等方面的关系，必须从样本中按月收入用分层抽样方法抽出100人作进一步分析，则月收入在[1 500,2 000)的这组中应抽取多少人？

    (2)试估计样本数据的中位数与平均数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，是双曲线C：的左，右焦点，O是坐标原点过作C的一条渐近线的垂线，垂足为P，若，则C的离心率为　　

    A. B. 2 C. D.

    查看答案和解析>>

    同步练习册答案