
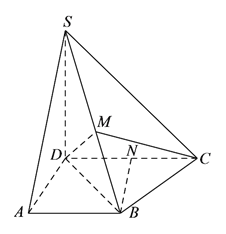
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 的中点为
的中点为![]() .
.
(![]() )求证:
)求证: ![]() 面
面![]() .
.
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )当
)当![]() 为何值时,能使
为何值时,能使![]() ?请给出证明.
?请给出证明.

【答案】证明见解析.
【解析】试题分析:(![]() )在直角梯形
)在直角梯形![]() 中,
中, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,易证
,易证![]() 平面
平面![]() .
.
(2)根据线面垂直的判定定理易证得AB⊥平面SAD,进而根据面面平行的判定定理易证得结论;
(3)分析可得当![]() 时,能使DM⊥MC,然后设CD的中点为P,连接BD,BP,再根据等腰三角形的性质易证得DM⊥SB,然后根据线面垂直的性质DM⊥BC,进而得到DM⊥平面SBC,从而证得结论.
时,能使DM⊥MC,然后设CD的中点为P,连接BD,BP,再根据等腰三角形的性质易证得DM⊥SB,然后根据线面垂直的性质DM⊥BC,进而得到DM⊥平面SBC,从而证得结论.
试题解析:(![]() )证明:∵在直角梯形
)证明:∵在直角梯形![]() 中,
中,
![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(![]() )证明:∵
)证明:∵![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 点,
点,
![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(![]() )当
)当![]() 时,有
时,有![]() ,
,
连接![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
设![]() 中点为
中点为![]() ,连接
,连接![]() ,且
,且![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
, ![]() ,
,
![]() 平面
平面![]() ,
, ![]() ,
,
∵![]() 点,
点,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 点,
点,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() .
.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】某客运公司用![]() 、
、![]() 两种型号的车辆承担甲、乙两地的长途客运业务,每车每天往返一次.
两种型号的车辆承担甲、乙两地的长途客运业务,每车每天往返一次.![]() 、
、![]() 两种型号的车辆的载客量分别是32人和48人,从甲地到乙地的营运成本依次为1500元/辆和2000元/辆.公司拟组建一个不超过21辆车的车队,并要求
两种型号的车辆的载客量分别是32人和48人,从甲地到乙地的营运成本依次为1500元/辆和2000元/辆.公司拟组建一个不超过21辆车的车队,并要求![]() 种型号的车不多于
种型号的车不多于![]() 种型号的车5辆.若每天从甲地运送到乙地的旅客不少于800人,为使公司从甲地到乙地的营运成本最小,应配备
种型号的车5辆.若每天从甲地运送到乙地的旅客不少于800人,为使公司从甲地到乙地的营运成本最小,应配备![]() 、
、![]() 两种型号的车各多少辆?并求出最小营运成本.
两种型号的车各多少辆?并求出最小营运成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论:
![]() “直线l与平面
“直线l与平面![]() 平行”是“直线l在平面
平行”是“直线l在平面![]() 外”的充分不必要条件;
外”的充分不必要条件;
![]() 若p:
若p:![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]() ;
;
![]() 命题“设a,
命题“设a,![]() ,若
,若![]() ,则
,则![]() 或
或![]() ”为真命题;
”为真命题;
![]() “
“![]() ”是“函数
”是“函数![]() 在
在![]() 上单调递增”的充要条件.
上单调递增”的充要条件.
其中所有正确结论的序号为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】采用系统抽样方法从![]() 人中抽取
人中抽取![]() 人做问卷调查,为此将他们随机编号为
人做问卷调查,为此将他们随机编号为![]() ,
,![]() ,
,![]() ,
,![]() ,分组后某组抽到的号码为41.抽到的
,分组后某组抽到的号码为41.抽到的![]() 人中,编号落入区间
人中,编号落入区间![]() 的人数为( )
的人数为( )
A. 10 B. ![]() C. 12 D. 13
C. 12 D. 13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com