
| A�� | $\sqrt{2}$ | B�� | $\frac{{\sqrt{6}}}{2}$ | C�� | $\frac{{\sqrt{5}}}{2}$ | D�� | $\sqrt{3}$ |
���� �������֪��-$\frac{1}{2{k}_{1}{k}_{2}}$+lnحk1ح+lnحk1ح=$\frac{1}{2{k}_{1}^{2}}$+ln${k}_{1}^{2}$����t=${k}_{1}^{2}$��t��0����g��t��=$\frac{1}{2t}$+lnt������ú����ĵ����ԣ���t=$\frac{1}{2}$ʱ��g��t��ȡ��Сֵ���ɻ�������ʽ�����ʿ�֪$\frac{2b}{a}$+$\frac{a}{b}$��2$\sqrt{2}$�����ҽ���a=$\sqrt{2}$b����a=$\sqrt{2}$b��k1=-k2=��$\frac{\sqrt{2}}{2}$ʱ��$\frac{2b}{a}+\frac{a}{b}-\frac{1}{{2{k_1}{k_2}}}+ln|{k_1}|+ln|{k_2}|$ȡ��Сֵʱ����e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{6}}{2}$��
��� �⣺�������֪��k1=-k2��0��
��-$\frac{1}{2{k}_{1}{k}_{2}}$+lnحk1ح+lnحk1ح=$\frac{1}{2{k}_{1}^{2}}$+ln${k}_{1}^{2}$��
��t=${k}_{1}^{2}$��t��0��
��g��t��=$\frac{1}{2t}$+lnt��
��g�䣨x��=$\frac{2t-1}{2{t}^{2}}$��
��g�䣨x����0����ã�x��$\frac{1}{2}$��
g�䣨x����0����ã�0��x��$\frac{1}{2}$��
��g��t��������������Ϊ��$\frac{1}{2}$��+�ޣ��������ݼ�����Ϊ��0��$\frac{1}{2}$����
�൱t=$\frac{1}{2}$ʱ����k1=��$\frac{\sqrt{2}}{2}$��g��t��ȡ��Сֵ��
��$\frac{2b}{a}$+$\frac{a}{b}$��2$\sqrt{2}$�����ҽ���a=$\sqrt{2}$b��
��$\frac{2b}{a}+\frac{a}{b}-\frac{1}{{2{k_1}{k_2}}}+ln|{k_1}|+ln|{k_2}|$���ҽ���t=$\frac{1}{2}$��a=$\sqrt{2}$bʱ�Ⱥţ�
��$\frac{2b}{a}+\frac{a}{b}-\frac{1}{{2{k_1}{k_2}}}+ln|{k_1}|+ln|{k_2}|$ȡ��Сֵ��������e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{6}}{2}$��
��ѡB��
���� ���⿼��˫���ߵļ������ʣ��������õ��������ĵ����Լ���ֵ�������������ʽ�����ʣ�������������������е��⣮


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��$\frac{1}{2}$�� | B�� | ��-1��1�� | C�� | ��-2��$\frac{1}{2}$�� | D�� | ��-1��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
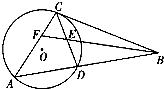 ��ͼ��D�ǡ�ABC��AB�ϵ�һ�㣬��ACD�ڽ���ԲO���ҡ�CAD=��BCD��E��CD���е㣬BE���ӳ��߽�AC�ڵ�F��֤����
��ͼ��D�ǡ�ABC��AB�ϵ�һ�㣬��ACD�ڽ���ԲO���ҡ�CAD=��BCD��E��CD���е㣬BE���ӳ��߽�AC�ڵ�F��֤�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | �٢ڢ� | B�� | �ڢ� | C�� | �٢ڢ� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 70 m | B�� | 72 m | C�� | 75 m | D�� | 80 m |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com