
已知函数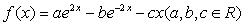 的导函数
的导函数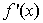 为偶函数,且曲线
为偶函数,且曲线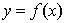 在点
在点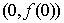 处的切线的斜率为
处的切线的斜率为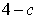 .
.
(Ⅰ)确定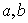 的值;
的值;
(Ⅱ)若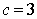 ,判断
,判断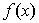 的单调性;
的单调性;
(Ⅲ)若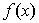 在
在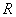 上是单调递增函数,求
上是单调递增函数,求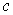 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
 某制造商某月内生产了一批乒乓球,随机抽样100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表:
某制造商某月内生产了一批乒乓球,随机抽样100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表:
| 分组 | 频数 | 频率 |
| [39.95,39.97) | 10 | |
| [39.97,39.99) | 30 | |
| [39.99,40.01) | 50 | |
| [40.01,40.03] | 10 | |
| 合计 | 100 |
(1) 请在上表中补充完成频率分布表,并在上图中画出频率分布直方图;
(2) 根据频率分布直方图,估计这批乒乓球直径的平均值(结果保留两位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题:①“所有能被2整除的整数都是偶数”的否定是“所有能被2整除的整数不都是偶数”②“菱形的两条对角线互相垂直”的逆 命题;③“
命题;③“ ,若
,若 ,则
,则 ”
” 的逆否命题;④“若
的逆否命题;④“若 ,则
,则 或
或 ”的否命题.上述命题中真命题的个数为
”的否命题.上述命题中真命题的个数为
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com