
分析 (1)去掉绝对值,讨论a的取值,求出f(x)的单调区间;
(2)由f(x)在[m,n]上的值域是[m,n]时,根据f(x)的单调性,列出对应的方程组,求出a的取值范围.
解答 解:(1)函数f(x)=|x2-a|(a∈R),
当a≤0时,f(x)=x2-a,
∴函数f(x)的单调递增区间为(0,+∞),
单调递减区间为(-∞,0);
当a>0时,令f(x)=0,解得x=±$\sqrt{a}$,
∴函数f(x)的单调递增区间为($\sqrt{a}$,+∞),(-$\sqrt{a}$,0),
单调递减区间为(-∞,-$\sqrt{a}$),(0,$\sqrt{a}$);
(2)假设存在实数m,n(m<n),使函数f(x)在[m,n]上的值域是[m,n],
①若m<n≤0,∵函数f(x)=|x2-a|≥0,∴结论不成立;
②若n>m≥0,假设函数f(x)=|x2-a|在区间[m,n]上存在两个和谐区间,
∵f(x)在(0,$\sqrt{a}$)上是减函数,($\sqrt{a}$,+∞)上是增函数,
∴$\left\{\begin{array}{l}{{m}^{2}-a=n}\\{{n}^{2}-a=m}\end{array}\right.$,消去a得m2-n2=n-m,
整理得(m-n)(m+n+1)=0;
因为m<n,所以m+n+1=0,即m=-n-1>0;∴n<-1,不合题意,应舍去;
或$\left\{\begin{array}{l}{{m}^{2}-a=m}\\{{n}^{2}-a=n}\end{array}\right.$,消去a得m2-n2=m-n,
整理得(m-n)(m+n-1)=0;
因为m<n,所以 m+n-1=0,即 n=1-m.
又$\left\{\begin{array}{l}{m≥0}\\{1-m>m}\end{array}\right.$,所以0≤m<$\frac{1}{2}$;
因为a=m2-m=${(m-\frac{1}{2})}^{2}$-$\frac{1}{4}$,所以-$\frac{1}{4}$<a≤0,不合题意,应舍去;
综上得,函数f(x)存在“和谐”区间时,a的取值范围是∅.
点评 本题考查了函数的单调性,新问题转化为函数的根的问题,求解难度较大,根据的关键是理解题意,把问题转化为求方程组或不等式组解的问题.


科目:高中数学 来源: 题型:选择题
| A. | p1<p2<$\frac{1}{2}$ | B. | ${p_1}<\frac{1}{2}<{p_2}$ | C. | p2<$\frac{1}{2}<{p_1}$ | D. | $\frac{1}{2}<{p_2}<{p_1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
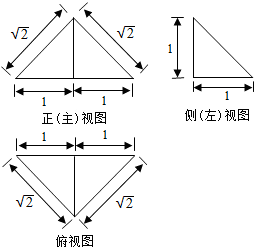
| A. | 1+$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 1+2$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆$\frac{x^2}{2}+{y^2}=1$上两个不同的点A,B关于直线y=mx+$\frac{1}{2}$对称.
已知椭圆$\frac{x^2}{2}+{y^2}=1$上两个不同的点A,B关于直线y=mx+$\frac{1}{2}$对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com