
���� �������A��ѧ������1��ѧ����ѡ�����ӵĶ����¼��ĸ��ʣ�Ȼ�������ʼ��ɣ�
�������X��ʾ���������������Ŀ���ֵ��������ʣ��õ�X�ķֲ��У�Ȼ�������ѧ������
��� �⣺���������⣬�μӼ�ѵ���С�Ůѧ������6�ˣ�����ѧ��ȫ��B�г�����ȼ���A��û��ѧ����ѡ�����ӣ��ĸ���Ϊ��$\frac{{C}_{3}^{3}{C}_{4}^{3}}{{C}_{6}^{3}{C}_{6}^{3}}$=$\frac{1}{100}$�����A��ѧ������1��ѧ����ѡ�����ӵĸ���Ϊ��1-$\frac{1}{100}$=$\frac{99}{100}$��
����ij������ǰ���Ӵ����ӵ�6����Ա�������ȡ4�˲�����X��ʾ����������������
��X�Ŀ���ȡֵΪ��1��2��3��
P��X=1��=$\frac{{C}_{3}^{1}{C}_{3}^{3}}{{C}_{6}^{4}}$=$\frac{1}{5}$��
P��X=2��=$\frac{{C}_{3}^{2}{C}_{3}^{2}}{{C}_{6}^{4}}$=$\frac{3}{5}$��
P��X=3��=$\frac{{C}_{3}^{3}{C}_{3}^{1}}{{C}_{6}^{4}}$=$\frac{1}{5}$��
X�ķֲ��У�
| X | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
���� ���⿼����ɢ����������ķֲ��У�������������ŵ�����ʵ���������������������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
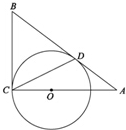 ��ͼ��AB��BC�ֱ���ԲO�����ڵ�D��C��AC����Բ��O����BC=2OC��
��ͼ��AB��BC�ֱ���ԲO�����ڵ�D��C��AC����Բ��O����BC=2OC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
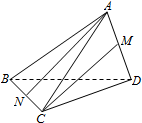 ��ͼ������A-BCD�У�AB=AC=BD=CD=3��AD=BC=2����M��N�ֱ���AD��BC���е㣬������ֱ��AN��CM���ɵĽǵ�����ֵ��$\frac{7}{8}$��
��ͼ������A-BCD�У�AB=AC=BD=CD=3��AD=BC=2����M��N�ֱ���AD��BC���е㣬������ֱ��AN��CM���ɵĽǵ�����ֵ��$\frac{7}{8}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������̨DEF-ABC�У�AB=2DE��G��H�ֱ�ΪAC��BC���е㣮
��ͼ��������̨DEF-ABC�У�AB=2DE��G��H�ֱ�ΪAC��BC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����ͼ��ԲO����AB��CD�ཻ�ڵ�E������A��ԲO��������DC���ӳ��߽��ڵ�P����PA=6��AE=9��PC=3��CE��ED=2��1����BE=2��
����ͼ��ԲO����AB��CD�ཻ�ڵ�E������A��ԲO��������DC���ӳ��߽��ڵ�P����PA=6��AE=9��PC=3��CE��ED=2��1����BE=2���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com