
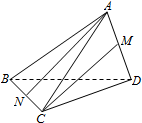
 如图,三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是$\frac{7}{8}$.
如图,三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是$\frac{7}{8}$. 分析 连结ND,取ND 的中点为:E,连结ME说明异面直线AN,CM所成的角就是∠EMC通过解三角形,求解即可.
解答 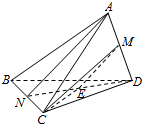 解:连结ND,取ND 的中点为:E,连结ME,则ME∥AN,异面直线AN,CM所成的角就是∠EMC,
解:连结ND,取ND 的中点为:E,连结ME,则ME∥AN,异面直线AN,CM所成的角就是∠EMC,
∵AN=2$\sqrt{2}$,
∴ME=$\sqrt{2}$=EN,MC=2$\sqrt{2}$,
又∵EN⊥NC,∴EC=$\sqrt{{EN}^{2}+{NC}^{2}}$=$\sqrt{3}$,
∴cos∠EMC=$\frac{{EM}^{2}+{MC}^{2}-{EC}^{2}}{2EM•MC}$=$\frac{2+8-3}{2×\sqrt{2}×2\sqrt{2}}$=$\frac{7}{8}$.
故答案为:$\frac{7}{8}$.
点评 本题考查异面直线所成角的求法,考查空间想象能力以及计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
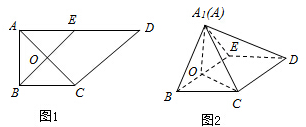 如图,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将ABE沿BE折起到A1BE的位置,如图2.
如图,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将ABE沿BE折起到A1BE的位置,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
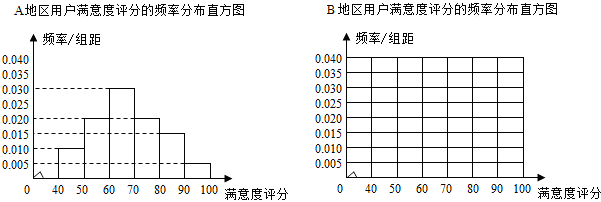
| 满意度评分分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 2 | 8 | 14 | 10 | 6 |
| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A′CD,所成二面角A′-CD-B的平面角为α,则( )
如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A′CD,所成二面角A′-CD-B的平面角为α,则( )| A. | ∠A′DB≤α | B. | ∠A′DB≥α | C. | ∠A′CB≤α | D. | ∠A′CB≥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com