
分析 如图所示,延长BA,CD交于点E,设AD=$\frac{1}{2}$x,AE=$\frac{\sqrt{2}}{2}$x,DE=$\frac{\sqrt{6}+\sqrt{2}}{4}$x,CD=m,求出$\frac{\sqrt{6}+\sqrt{2}}{4}$x+m=$\sqrt{6}$+$\sqrt{2}$,即可求出AB的取值范围.
解答 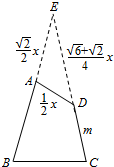 解:方法一:
解:方法一:
如图所示,延长BA,CD交于点E,则
在△ADE中,∠DAE=105°,∠ADE=45°,∠E=30°,
∴设AD=$\frac{1}{2}$x,AE=$\frac{\sqrt{2}}{2}$x,DE=$\frac{\sqrt{6}+\sqrt{2}}{4}$x,CD=m,
∵BC=2,
∴($\frac{\sqrt{6}+\sqrt{2}}{4}$x+m)sin15°=1,
∴$\frac{\sqrt{6}+\sqrt{2}}{4}$x+m=$\sqrt{6}$+$\sqrt{2}$,
∴0<x<4,
而AB=$\frac{\sqrt{6}+\sqrt{2}}{4}$x+m-$\frac{\sqrt{2}}{2}$x=$\sqrt{6}$+$\sqrt{2}$-$\frac{\sqrt{2}}{2}$x,
∴AB的取值范围是($\sqrt{6}$-$\sqrt{2}$,$\sqrt{6}$+$\sqrt{2}$).
故答案为:($\sqrt{6}$-$\sqrt{2}$,$\sqrt{6}$+$\sqrt{2}$).
方法二:
如下图,作出底边BC=2的等腰三角形EBC,B=C=75°,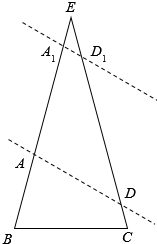
倾斜角为150°的直线在平面内移动,分别交EB、EC于A、D,则四边形ABCD即为满足题意的四边形;
当直线移动时,运用极限思想,
①直线接近点C时,AB趋近最小,为$\sqrt{6}$-$\sqrt{2}$;
②直线接近点E时,AB趋近最大值,为$\sqrt{6}$+$\sqrt{2}$;
故答案为:($\sqrt{6}$-$\sqrt{2}$,$\sqrt{6}$+$\sqrt{2}$).
点评 本题考查求AB的取值范围,考查三角形中的几何计算,考查学生的计算能力,属于中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
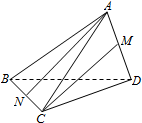 如图,三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是$\frac{7}{8}$.
如图,三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是$\frac{7}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1是f(x)的零点 | B. | 1是f(x)的极值点 | ||
| C. | 3是f(x)的极值 | D. | 点(2,8)在曲线y=f(x)上 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如题图,圆O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6,AE=9,PC=3,CE:ED=2:1,则BE=2.
如题图,圆O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6,AE=9,PC=3,CE:ED=2:1,则BE=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com