
| A. | p1<p2<$\frac{1}{2}$ | B. | ${p_1}<\frac{1}{2}<{p_2}$ | C. | p2<$\frac{1}{2}<{p_1}$ | D. | $\frac{1}{2}<{p_2}<{p_1}$ |
分析 分别求出事件“x+y≤$\frac{1}{2}$”和事件“xy≤$\frac{1}{2}$”对应的区域,然后求出面积,利用几何概型公式求出概率,比较大小.
解答 解:由题意,事件“x+y≤$\frac{1}{2}$”表示的区域如图阴影三角形,
p1=$\frac{\frac{1}{2}×\frac{1}{2}×\frac{1}{2}}{1}=\frac{1}{8}$;
满足事件“xy≤$\frac{1}{2}$”的区域如图阴影部分
所以p2=$\frac{1×\frac{1}{2}+{∫}_{\frac{1}{2}}^{1}\frac{1}{2x}dx}{1}$=$\frac{1}{2}+\frac{1}{2}lnx{|}_{\frac{1}{2}}^{1}$=$\frac{1}{2}(1+ln2)$>$\frac{1}{2}$;
所以${p}_{1}<\frac{1}{2}<{p}_{2}$;
故选:B.
点评 本题考查了几何概型的公式运用;关键是分别求出阴影部分的面积,利用几何概型公式解答.


科目:高中数学 来源: 题型:选择题
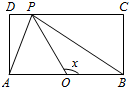 如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )
如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )| A. | 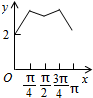 | B. | 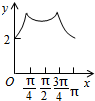 | C. | 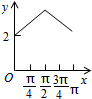 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3})$ | B. | $(-\frac{\sqrt{3}}{6},\frac{\sqrt{3}}{6})$ | C. | $(-\frac{2\sqrt{2}}{3},\frac{2\sqrt{2}}{3})$ | D. | $(-\frac{2\sqrt{3}}{3},\frac{2\sqrt{3}}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 134石 | B. | 169石 | C. | 338石 | D. | 1365石 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 18 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com