
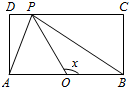
 如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )
如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )| A. | 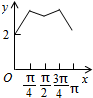 | B. | 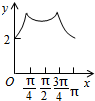 | C. | 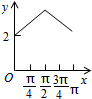 | D. | 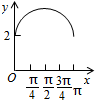 |
分析 根据函数图象关系,利用排除法进行求解即可.
解答 解:当0≤x≤$\frac{π}{4}$时,BP=tanx,AP=$\sqrt{A{B}^{2}+B{P}^{2}}$=$\sqrt{4+ta{n}^{2}x}$,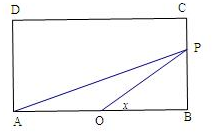
此时f(x)=$\sqrt{4+ta{n}^{2}x}$+tanx,0≤x≤$\frac{π}{4}$,此时单调递增,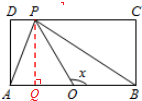
当P在CD边上运动时,$\frac{π}{4}$≤x≤$\frac{3π}{4}$且x≠$\frac{π}{2}$时,
如图所示,tan∠POB=tan(π-∠POQ)=tanx=-tan∠POQ=-$\frac{PQ}{OQ}$=-$\frac{1}{OQ}$,
∴OQ=-$\frac{1}{tanx}$,
∴PD=AO-OQ=1+$\frac{1}{tanx}$,PC=BO+OQ=1-$\frac{1}{tanx}$,
∴PA+PB=$\sqrt{(1-\frac{1}{tanx})^{2}+1}+\sqrt{(1+\frac{1}{tanx})^{2}+1}$,
当x=$\frac{π}{2}$时,PA+PB=2$\sqrt{2}$,
当P在AD边上运动时,$\frac{3π}{4}$≤x≤π,PA+PB=$\sqrt{4+ta{n}^{2}x}$-tanx,
由对称性可知函数f(x)关于x=$\frac{π}{2}$对称,
且f($\frac{π}{4}$)>f($\frac{π}{2}$),且轨迹为非线型,
排除A,C,D,
故选:B.
点评 本题主要考查函数图象的识别和判断,根据条件先求出0≤x≤$\frac{π}{4}$时的解析式是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 最小值为0,无最大值 | B. | 最小值为0,最大值为6 | ||
| C. | 最小值为-$\frac{1}{4}$,无最大值 | D. | 最小值为-$\frac{1}{4}$,最大值为6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 200 | B. | 150 | C. | 100 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{8}{9π}$ | B. | $\frac{8}{27π}$ | C. | $\frac{24(\sqrt{2}-1)^{3}}{π}$ | D. | $\frac{8(\sqrt{2}-1)^{3}}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形.
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p1<p2<$\frac{1}{2}$ | B. | ${p_1}<\frac{1}{2}<{p_2}$ | C. | p2<$\frac{1}{2}<{p_1}$ | D. | $\frac{1}{2}<{p_2}<{p_1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com