
| A. | 200 | B. | 150 | C. | 100 | D. | 50 |
分析 对于集合E,s=4时,p,q,r从0,1,2,3任取一数都有4种取法,从而构成的元素(p,q,r,s)有4×4×4=64个,再讨论s=3,2,1的情况,求法一样,把每种情况下元素个数相加即可得到集合E的元素个数,而对于集合F,需讨论两个数:u,w,方法类似,最后把求得的集合E,F元素个数相加即可.
解答 解:(1)s=4时,p,q,r的取值的排列情况有4×4×4=64种;
s=3时,p,q,r的取值的排列情况有3×3×3=27种;
s=2时,有2×2×2=8种;
s=1时,有1×1×1=1种;
∴card(E)=64+27+8+1=100;
(2)u=4时:若w=4,t,v的取值的排列情况有4×4=16种;
若w=3,t,v的取值的排列情况有4×3=12种;
若w=2,有4×2=8种;
若w=1,有4×1=4种;
u=3时:若w=4,t,v的取值的排列情况有3×4=12种;
若w=3,t,v的取值的排列情况有3×3=9种;
若w=2,有3×2=6种;
若w=1,有3×1=3种;
u=2时:若w=4,t,v的取值的排列情况有2×4=8种;
若w=3,有2×3=6种;
若w=2,有2×2=4种;
若w=1,有2×1=2种;
u=1时:若w=4,t,v的取值的排列情况有1×4=4种;
若w=3,有1×3=3种;
若w=2,有1×2=2种;
若w=1,有1×1=1种;
∴card(F)=100;
∴card(E)+card(F)=200.
故选A.
点评 考查描述法表示集合,分布计数原理的应用,注意要弄清讨论谁,做到不重不漏.


科目:高中数学 来源: 题型:解答题
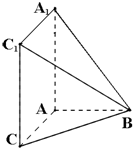 如图,在四棱锥B-AA1C1C中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在四棱锥B-AA1C1C中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
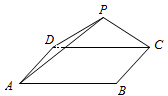 如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.
如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
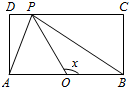 如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )
如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )| A. | 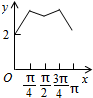 | B. | 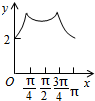 | C. | 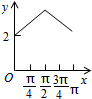 | D. | 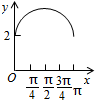 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com