
分析 (I)由a4-a3=2,可求公差d,然后由a1+a2=10,可求a1,结合等差数列的通项公式可求
(II)由b2=a3=8,b3=a7=16,可求等比数列的首项及公比,代入等比数列的通项公式可求b6,结合(I)可求
解答 解:(I)设等差数列{an}的公差为d.
∵a4-a3=2,所以d=2
∵a1+a2=10,所以2a1+d=10
∴a1=4,
∴an=4+2(n-1)=2n+2(n=1,2,…)
(II)设等比数列{bn}的公比为q,
∵b2=a3=8,b3=a7=16,
∴$\left\{\begin{array}{l}{{b}_{1}q=8}\\{{b}_{1}{q}^{2}=16}\end{array}\right.$
∴q=2,b1=4
∴${b}_{6}=4×{2}^{6-1}$=128,而128=2n+2
∴n=63
∴b6与数列{an}中的第63项相等
点评 本题主要考查了等差数列与等比数列通项公式的简单应用,属于对基本公式应用的考查,试题比较容易.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 200 | B. | 150 | C. | 100 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 类别 | 人数 |
| 老年教师 | 900 |
| 中年教师 | 1800 |
| 青年教师 | 1600 |
| 合计 | 4300 |
| A. | 90 | B. | 100 | C. | 180 | D. | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{8}{9π}$ | B. | $\frac{8}{27π}$ | C. | $\frac{24(\sqrt{2}-1)^{3}}{π}$ | D. | $\frac{8(\sqrt{2}-1)^{3}}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
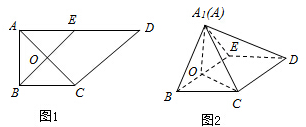 如图,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将ABE沿BE折起到A1BE的位置,如图2.
如图,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将ABE沿BE折起到A1BE的位置,如图2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com