
分析 利用双曲线的定义,确定△APF周长最小时,P的坐标,即可求出△APF周长最小时,该三角形的面积.
解答 解:由题意,设F′是左焦点,则△APF周长=|AF|+|AP|+|PF|=|AF|+|AP|+|PF′|+2
≥|AF|+|AF′|+2(A,P,F′三点共线时,取等号),
直线AF′的方程为$\frac{x}{-3}+\frac{y}{6\sqrt{6}}=1$与x2-$\frac{{y}^{2}}{8}$=1联立可得y2+6$\sqrt{6}$y-96=0,
∴P的纵坐标为2$\sqrt{6}$,
∴△APF周长最小时,该三角形的面积为$\frac{1}{2}×6×6\sqrt{6}$-$\frac{1}{2}×6×2\sqrt{6}$=12$\sqrt{6}$.
故答案为:12$\sqrt{6}$.
点评 本题考查双曲线的定义,考查三角形面积的计算,确定P的坐标是关键.


 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
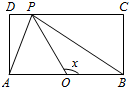 如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )
如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )| A. | 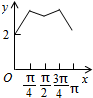 | B. | 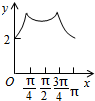 | C. | 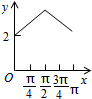 | D. | 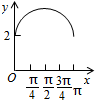 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
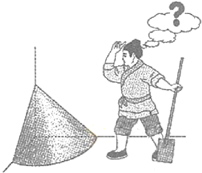 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:”今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?“其意思为:”在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?“已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:”今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?“其意思为:”在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?“已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )| A. | 14斛 | B. | 22斛 | C. | 36斛 | D. | 66斛 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{21}$ | B. | $\frac{10}{21}$ | C. | $\frac{11}{21}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3})$ | B. | $(-\frac{\sqrt{3}}{6},\frac{\sqrt{3}}{6})$ | C. | $(-\frac{2\sqrt{2}}{3},\frac{2\sqrt{2}}{3})$ | D. | $(-\frac{2\sqrt{3}}{3},\frac{2\sqrt{3}}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 18 | D. | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com