
分析 根据题意,结合题意双曲线的渐近线过点(3,-4),可得其一条渐近线方程,分2种情况讨论,若双曲线的焦点在x轴上,分析可得$\frac{b}{a}$=$\frac{4}{3}$,即b=$\frac{4}{3}$a,由双曲线的几何性质可得c=$\sqrt{{a}^{2}+{b}^{2}}$=$\frac{5}{3}$a,由离心率公式计算可得此时双曲线离心率,若双曲线的焦点在y轴上,同理分析可得此时双曲线离心率,综合可得答案.
解答 解:根据题意,若该双曲线的渐进线过点(3,-4),则其一条渐近线方程为:y=-$\frac{4}{3}$x,
分2种情况讨论:
若双曲线的焦点在x轴上,设双曲线的方程为:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,则其渐近线方程为y=±$\frac{b}{a}$x,
则有$\frac{b}{a}$=$\frac{4}{3}$,即b=$\frac{4}{3}$a,
则c=$\sqrt{{a}^{2}+{b}^{2}}$=$\frac{5}{3}$a,
则其离心率e=$\frac{c}{a}$=$\frac{5}{3}$;
若双曲线的焦点在y轴上,设双曲线的方程为:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1,则其渐近线方程为y=±$\frac{a}{b}$x,
则有$\frac{a}{b}$=$\frac{4}{3}$,即b=$\frac{3}{4}$a,
则c=$\sqrt{{a}^{2}+{b}^{2}}$=$\frac{5}{4}$a,
则其离心率e=$\frac{c}{a}$=$\frac{5}{4}$;
综合可得:双曲线的离心率为$\frac{5}{3}$或$\frac{5}{4}$.
故答案为:$\frac{5}{3}$或$\frac{5}{4}$.
点评 本题考查双曲线的几何性质,注意双曲线的焦点的位置.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$-1 | B. | 1+$\sqrt{6}$ | C. | $\sqrt{3}$-1 | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,$\frac{2}{3}$) | B. | (1,$\frac{3}{2}$) | C. | ($\frac{4}{3}$,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男生 | 女生 | 合计 | |
| 挑同桌 | 30 | 40 | 70 |
| 不挑同桌 | 20 | 10 | 30 |
| 总计 | 50 | 50 | 100 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
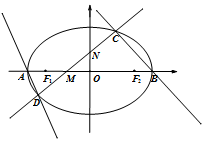 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com