(I)解:设P(x,y),
∵动点P到两点(0,-

),(0,

)的距离之和等于4
∴由椭圆定义可知,点P的轨迹C是以(0,-

),(0,

)为焦点,长半轴为2的椭圆.它的短半轴b=

=1,故曲线C的方程为x2+

=1.
(Ⅱ)解:设A(x
1,y
1),B(x
2,y
2),
由以AB为直径的圆过原点0,可得OA⊥OB,∴x
1x
2+y
1y
2=0
将直线y=kx+l代入椭圆方程,消元可得(4+k
2)x
2+2kx-3=0
∴x
1+x
2=-
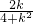
,x
1x
2=-
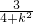
∴y
1y
2=(kx
1+l)(kx
2+l)=
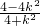
∴-
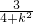
+
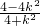
=0
∴

,∴k=

;
(Ⅲ)证明:
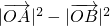
=(
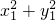
)-(
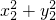
)=
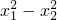
+
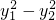
=
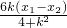
∵点A在第一象限,∴x
1>0
∵x
1x
2=-
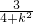
,∴x
2<0
∴x
1-x
2>0
∵k>0,∴
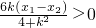
,
∴恒有|OA|>|OB|.
分析:(I)动点P到两点(0,-

),(0,

)的距离之和等于4,由椭圆的定义知此动点的轨迹应为椭圆,从而可得动点的轨迹方程;
(Ⅱ)设A(x
1,y
1),B(x
2,y
2),由以AB为直径的圆过原点0,可得OA⊥OB,从而x
1x
2+y
1y
2=0,将直线y=kx+l代入椭圆方程,消元可得一元二次方程,利用韦达定理,即可求k的值;
(Ⅲ)用坐标表示出
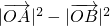
,利用点A在第一象限,k>0,即可证得结论.
点评:本题考查了利用定义法求动点的轨迹方程,考查直线与椭圆的位置关系,考查不等式的证明,关键要理解好椭圆定义的条件,正确运用韦达定理进行解题.

 ),(0,
),(0, )的距离之和等于4,设点P的轨迹为C,已知直线y=kx+l与C交于A、B两点.
)的距离之和等于4,设点P的轨迹为C,已知直线y=kx+l与C交于A、B两点. ),(0,
),(0, )的距离之和等于4
)的距离之和等于4 ),(0,
),(0, )为焦点,长半轴为2的椭圆.它的短半轴b=
)为焦点,长半轴为2的椭圆.它的短半轴b= =1,故曲线C的方程为x2+
=1,故曲线C的方程为x2+ =1.
=1.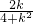 ,x1x2=-
,x1x2=-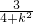
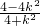
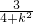 +
+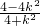 =0
=0 ,∴k=
,∴k= ;
;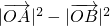 =(
=(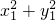 )-(
)-(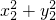 )=
)=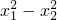 +
+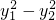 =
=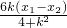
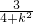 ,∴x2<0
,∴x2<0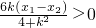 ,
, ),(0,
),(0, )的距离之和等于4,由椭圆的定义知此动点的轨迹应为椭圆,从而可得动点的轨迹方程;
)的距离之和等于4,由椭圆的定义知此动点的轨迹应为椭圆,从而可得动点的轨迹方程;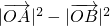 ,利用点A在第一象限,k>0,即可证得结论.
,利用点A在第一象限,k>0,即可证得结论.

 如图,正方体ABCD-A1B1C1D1的棱长为1,点M在AB上,且AM=
如图,正方体ABCD-A1B1C1D1的棱长为1,点M在AB上,且AM=