
函数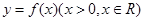 ,满足
,满足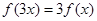 ,若
,若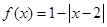 ,
,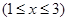 ,则集合
,则集合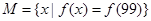 中最小的元素是 .
中最小的元素是 .
45
解析试题分析:解:(1)∵当1≤x≤3时,f(x)=1﹣|x﹣2|,
∴当3≤x≤9时,f(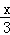 )=1﹣|
)=1﹣|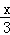 ﹣2|,可得f(
﹣2|,可得f(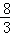 )=1﹣|
)=1﹣|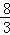 ﹣2|=
﹣2|= ,
,
又∵对任意x≥1,都有f(3x)=3f(x),根据题意,得当3≤x≤9时,f(x)=3f(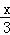 )=3﹣|3x﹣6|;
)=3﹣|3x﹣6|;
当9≤x≤27时,f(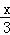 )=3﹣|3•
)=3﹣|3•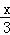 ﹣6|=3﹣|x﹣6|,此时f(x)=3f(
﹣6|=3﹣|x﹣6|,此时f(x)=3f(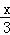 )=9﹣|3x﹣18|;
)=9﹣|3x﹣18|;
当27≤x≤81时,f(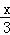 )=9﹣|3•
)=9﹣|3•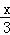 ﹣18|=9﹣|x﹣18|,此时f(x)=3f(
﹣18|=9﹣|x﹣18|,此时f(x)=3f(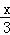 )=27﹣|3x﹣54|;
)=27﹣|3x﹣54|;
当81≤x≤243时,f(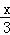 )=27﹣|3•
)=27﹣|3•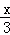 ﹣54|=27﹣|x﹣54|,此时f(x)=3f(
﹣54|=27﹣|x﹣54|,此时f(x)=3f(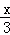 )=81﹣|3x﹣162|.
)=81﹣|3x﹣162|.
由此可得f(99)=81﹣|3×99﹣162|=﹣54接下来解方程f(x)=﹣54:
当27≤x≤81时,27﹣|3x﹣54|=﹣54,得3x﹣54=±81,所以x=45(舍负);
当9≤x≤27时,9﹣|3x﹣18|=﹣54,得3x﹣18=±63,找不到符合条件的x;
当3≤x≤9时,3﹣|3x﹣6|=﹣54,得3x﹣6=±57,找不到符合条件的x.
因此集合M={x|f(x)=f(99)}中最小的元素是45
故答案为45
考点:函数解析式
点评:本题考查了利用给出的关系式求函数值,因自变量不在定义域内,需要根据关系式进行转化,再代入求值,这是常用的一种方法.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:填空题
已知函数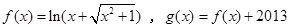 ,下列命题:
,下列命题:
① 的定义域为
的定义域为 ;
;
② 是奇函数;
是奇函数;
③ 在
在 单调递增;
单调递增;
④若实数a,b满足 ,则
,则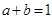 ;
;
⑤设函数 在
在 的最大值为M,最小值为m,则M+m=2013
的最大值为M,最小值为m,则M+m=2013
其中真命题的序号是 (写出所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com