
【题目】已知点F是拋物线C:y2=2px(p>0)的焦点,点M(x0,1)在C上,且|MF|=![]() .
.
(1)求p的值;
(2)若直线l经过点Q(3,-1)且与C交于A,B(异于M)两点,证明:直线AM与直线BM的斜率之积为常数.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)抛物线定义知|![]() ,则
,则![]() ,求得x0=2p,代入抛物线方程,
,求得x0=2p,代入抛物线方程,![]() ;
;
(2)由(1)得M(1,1),拋物线C:y2=2x,
当直线l经过点Q(3,-1)且垂直于x轴时,直线AM的斜率![]() ,直线BM的斜率
,直线BM的斜率![]() ,
,![]() .
.
当直线l不垂直于x轴时,直线l的方程为y+1=k(x-3),代入抛物线方程,由韦达定理及斜率公式求得![]() ,即可证明直线AM与直线BM的斜率之积为常数
,即可证明直线AM与直线BM的斜率之积为常数![]() .
.
(1)由抛物线定义知|MF|=x0+,则x0+=x0,解得x0=2p,
又点M(x0,1)在C上,所以2px0=1,解得x0=1,p=.
(2)由(1)得M(1,1),C:y2=x.
当直线l经过点Q(3,-1)且垂直于x轴时,不妨设A(3,![]() ),B(3,-
),B(3,-![]() ),
),
则直线AM的斜率kAM=![]() ,直线BM的斜率kBM=
,直线BM的斜率kBM=![]() ,所以kAM·kBM=-
,所以kAM·kBM=-![]() ×
×![]() =-.
=-.
当直线l不垂直于x轴时,设A(x1,y1),B(x2,y2),
则直线AM的斜率kAM=![]() =
=![]() =
=![]() ,同理直线BM的斜率kBM=
,同理直线BM的斜率kBM=![]() ,∴kAM·kBM=
,∴kAM·kBM=![]() ·
·![]() =
=![]() .
.
设直线l的斜率为k(显然k≠0且k≠-1),则直线l的方程为y+1=k(x-3).
联立![]() 消去x,得ky2-y-3k-1=0,
消去x,得ky2-y-3k-1=0,
所以y1+y2=,y1y2=-![]() =-3-,故kAM·kBM=
=-3-,故kAM·kBM=![]() =
=![]() =-.
=-.
综上,直线AM与直线BM的斜率之积为-.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,动点![]() 到两坐标轴的距离之和等于它到定点
到两坐标轴的距离之和等于它到定点![]() 的距离,记点P的轨迹为
的距离,记点P的轨迹为![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() 关于原点对称;②
关于原点对称;②![]() 关于直线
关于直线![]() 对称;③直线
对称;③直线![]() 与
与![]() 有无数个公共点;④在第一象限内,
有无数个公共点;④在第一象限内,![]() 与x轴和y轴所围成的封闭图形的面积小于
与x轴和y轴所围成的封闭图形的面积小于![]() .其中正确的结论是________.(写出所有正确结论的序号)
.其中正确的结论是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一块长方形区域![]() ,
,![]() ,
,![]() ,在边
,在边![]() 的中点
的中点![]() 处有一个可转动的探照灯,其照射角
处有一个可转动的探照灯,其照射角![]() 始终为
始终为![]() ,设
,设![]() ,探照灯照射在长方形
,探照灯照射在长方形![]() 内部区域的面积为
内部区域的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,求
时,求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的不等式
的不等式![]() 有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数
有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数![]() 的取值范围是( )
的取值范围是( )
A. (![]() ,
,![]() ] B. (
] B. (![]() ,
,![]() ] C. [
] C. [![]() ,
,![]() ) D. [
) D. [![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
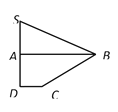
【题目】已知四边形![]() ,点
,点![]() 为线段
为线段![]() 的中点,且
的中点,且![]()
![]() .
. ![]() ,
, ![]() .现将△
.现将△![]() 沿
沿![]() 进行翻折,使得
进行翻折,使得![]()
![]() °,得到图形如图所示,连接
°,得到图形如图所示,连接![]() .
.
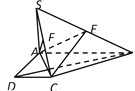
(Ⅰ)若点![]() 在线段
在线段![]() 上,证明:
上,证明: ![]() ;
;
(Ⅱ)若![]() 点为
点为![]() 的中点,求点
的中点,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com