
【题目】如图,已知菱形![]() 和矩形
和矩形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() .
.

(1)求直线![]() 与平面
与平面![]() 的夹角;
的夹角;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1) ![]() . (2)
. (2) ![]()
【解析】
设![]() ,以
,以![]() 点为坐标原点,以
点为坐标原点,以![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,过
轴,过![]() 点且平行于
点且平行于![]() 的方向为
的方向为![]() 轴正方向,建立空间坐标系,
轴正方向,建立空间坐标系,
(1)由题意,求出直线![]() 的方向向量,平面
的方向向量,平面![]() 的一个法向量,由向量夹角,即可得到直线与平面夹角;
的一个法向量,由向量夹角,即可得到直线与平面夹角;
(2)先求出平面![]() 的一个法向量
的一个法向量![]() ,由点
,由点![]() 到平面
到平面![]() 的距离
的距离 ,即可求出结果.
,即可求出结果.
设![]() ,因为菱形
,因为菱形![]() 和矩形
和矩形![]() 所在的平面互相垂直,所以易得
所在的平面互相垂直,所以易得![]() 平面
平面![]() ;以
;以![]() 点为坐标原点,以
点为坐标原点,以![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,过
轴,过![]() 点且平行于
点且平行于![]() 的方向为
的方向为![]() 轴正方向,建立空间坐标系,
轴正方向,建立空间坐标系,
(1)由已知得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
因为![]() 轴垂直于平面
轴垂直于平面![]() ,
,
因此可令平面![]() 的一个法向量为
的一个法向量为![]() ,又
,又![]() ,
,
设直线![]() 与平面
与平面![]() 的夹角为
的夹角为![]() ,
,
则有 ,
,
即![]() ,
,
所以直线BF与平面ABCD的夹角为![]() .
.
(2)因为![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
 ,令
,令![]() 得
得![]() ,
,
又因为![]() ,
,
所以点![]() 到平面
到平面![]() 的距离
的距离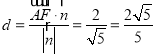 .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标![]() 系中,直线
系中,直线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]() .
.
(1)①当![]() 时,写出直线
时,写出直线![]() 的普通方程;
的普通方程;
②写出曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() ,设曲线
,设曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() 最小值.
最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系原点为极点,以
为参数).以直角坐标系原点为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地需要修建一条大型输油管道通过120公里宽的沙漠地带,该段输油管道两端的输油站已建好,余下工程只需要在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站)。经预算,修建一个增压站的工程费用为400万元,铺设距离为![]() 公里的相邻两增压站之间的输油管道费用为
公里的相邻两增压站之间的输油管道费用为![]() 万元。设余下工程的总费用为
万元。设余下工程的总费用为![]() 万元。
万元。
(I)试将![]() 表示成关于
表示成关于![]() 的函数;
的函数;
(II)需要修建多少个増压站才能使总费用![]() 最小?
最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为研究学生玩电脑游戏和对待作业量态度的关系,随机抽取了100名学生进行调查,所得数据如下表所示:
认为作业多 | 认为作业不多 | 总计 | |
喜欢玩电脑游戏 | 25 | 15 | 40 |
不喜欢玩电脑游戏 | 25 | 35 | 60 |
总计 | 50 | 50 | 100 |
(参考公式![]() ,可能用到数据:
,可能用到数据:![]() ,
,![]() ),参照以上公式和数据,得到的正确结论是( )
),参照以上公式和数据,得到的正确结论是( )
A. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度有关
的把握认为喜欢玩电脑游戏与对待作业量的态度有关
B. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度无关
的把握认为喜欢玩电脑游戏与对待作业量的态度无关
C. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度有关
的把握认为喜欢玩电脑游戏与对待作业量的态度有关
D. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度无关
的把握认为喜欢玩电脑游戏与对待作业量的态度无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若对于
,若对于![]() 分别为某个三角形的边长,则称
分别为某个三角形的边长,则称![]() 为“三角形函数”.给出下列四个函数:
为“三角形函数”.给出下列四个函数:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中为“三角形函数”的个数是( )
.其中为“三角形函数”的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 为
为![]() 上任意一点,
上任意一点,![]() 为菱形
为菱形![]() 对角线的交点。
对角线的交点。
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,当四棱锥的体积被平面
,当四棱锥的体积被平面![]() 分成3:1两部分时,若二面角
分成3:1两部分时,若二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值。
的值。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是网格工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行,数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,若数字195在第m行从左至右算第n个数字,则![]() 为_______.
为_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() 分别是
分别是![]() 的中点将
的中点将![]() 分别沿
分别沿![]() 折起,使
折起,使![]() 重合于点
重合于点![]() .则下列结论正确的是( )
.则下列结论正确的是( )

A. ![]()
B. 平面![]()
C. 二面角![]() 的余弦值为
的余弦值为![]()
D. 点![]() 在平面
在平面![]() 上的投影是
上的投影是![]() 的外心
的外心
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com