
分析 由已知的A,a,b,根据正弦定理表示出sinB,
(1)由A为钝角或直角,得到B一定为锐角,即A大于B,根据大角对大边可得a大于b,与已知的条件a小于等于b矛盾,故此三角形不存在,本选项正确;
(2)把A,a及b的值代入表示出的sinB,确定出sinB的值,由A为钝角或直角,得到B为锐角,故B的角度只有一解,本选项正确;
(3)当A=60°,a=1,b=3,得sinB=$\frac{bsinA}{a}$=$\frac{3×sin60°}{1}$=$\frac{3\sqrt{3}}{2}>1$,此三角形不存在,本选项正确;
(4)由A为锐角,把a=bsinA代入表示出的sinB中,得到其值为1,根据B为三角形的内角,可得出B为直角,从而得到三角形为直角三角形,本选项正确;
(5)取一个特例:a=b时,A=B,由A为锐角,得到B也为锐角,此三角形只有一解,本选项错误.
解答 解:由A,a,b已知,根据正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$得:sinB=$\frac{bsinA}{a}$,
(1)若A≥90°,根据大角对大边得a>b,故a≤b时,此三角形不存在,本选项正确;
(2)由A≥90°,根据大角对大边得a>b,进而得到B为锐角,即此三角形最多有一解,本选项正确;
(3)当A=60°,a=1,b=3,得sinB=$\frac{bsinA}{a}$=$\frac{3×sin60°}{1}$=$\frac{3\sqrt{3}}{2}>1$,此三角形不存在,本选项正确;
(4)若A<90°,且a=bsinA,得到sinB=1,由B为三角形的内角,得到B=90°,此三角形为直角三角形,本选项正确;
(5)当a=b时,A=B,此三角形为等腰三角形,只有一解,当A<90°,且bsinA<a≤b时,三角形不一定有两解,本选项错误,
故答案为:(1)(2)(3)(4).
点评 此题考查了正弦定理的应用,正弦函数的值域以及三角形的边角关系,要说明一个命题是真命题,必须经过严格证明,要说明一个命题为假命题,只需举一个反例即可,熟练掌握正弦定理是解本题的关键,本题属于中档题.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆 | B. | 抛物线 | C. | 椭圆 | D. | 双曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2-i | B. | -1+2i | C. | 1+2i | D. | -1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
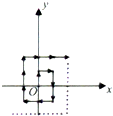 如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )
如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )| A. | (-21,12) | B. | (-22,12) | C. | (-21,13) | D. | (-22,13) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | $-\frac{7}{25}$ | C. | $\frac{24}{25}$ | D. | $-\frac{24}{25}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com