
【题目】某少数民族的刺绣有着悠久的历史,下图![]() 为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含
为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含![]() 个小正方形.
个小正方形.

(1)求出![]() ;
;
(2)利用合情推理的“归纳推理思想”归纳出![]() 与
与![]() 的关系式,
的关系式,
(3)根据你得到的关系式求![]() 的表达式
的表达式
【答案】(1)41(2)f(n)=2n2﹣2n+1.
【解析】【试题分析】(1)先求出![]() ,找出规律
,找出规律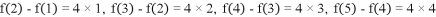 ,求出
,求出![]() ;(2)借助归纳推理找出规律:
;(2)借助归纳推理找出规律:![]() -
-![]() ;(3)借助(2)的规律
;(3)借助(2)的规律![]() -
-![]() 运用两边叠加的方法求解:
运用两边叠加的方法求解:
解:(Ⅰ)∵f(1)=1,f(2)=5,f(3)=13,f(4)=25,
∴f(2)﹣f(1)=4=4×1.
f(3)﹣f(2)=8=4×2,
f(4)﹣f(3)=12=4×3,
f(5)﹣f(4)=16=4×4
∴f(5)=25+4×4=41.
(Ⅱ)由上式规律得出f(n+1)﹣f(n)=4n.
∴f(2)﹣f(1)=4×1,
f(3)﹣f(2)=4×2,
f(4)﹣f(3)=4×3,
…
f(n﹣1)﹣f(n﹣2)=4(n﹣2),
f(n)﹣f(n﹣1)=4(n﹣1)
∴f(n)﹣f(1)=4[1+2+…+(n﹣2)+(n﹣1)]=2(n﹣1)n,
∴f(n)=2n2﹣2n+1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】有4个不同的球,4个不同的盒子,把球全部放入盒子内.
(1)共有几种放法?
(2)恰有1个空盒,有几种放法?
(3)恰有2个盒子不放球,有几种放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率.
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年夏季奥运会将在巴西里约热内卢举行,体育频道为了解某地区关于
奥运会直播的收视情况,随机抽取了![]() 名观众进行调查,其中
名观众进行调查,其中![]() 岁以上的观众有
岁以上的观众有![]() 名,下面是根据
名,下面是根据
调查结果绘制的观众准备平均每天收看奥运会直播时间的频率分布表(时间:分钟):
分组 |
|
|
|
|
|
|
频率 |
|
|
|
|
|
|
将每天准备收看奥运会直播的时间不低于![]() 分钟的观众称为“奥运迷”,已知“奥运迷”中有
分钟的观众称为“奥运迷”,已知“奥运迷”中有![]() 名
名![]() 岁
岁
以上的观众.
(1)根据已知条件完成下面的![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 以上的把握认为“奥运迷”与年龄
以上的把握认为“奥运迷”与年龄
有关?
非“奥运迷” | “奥运迷” | 合计 | |
| |||
| |||
合计 |
(2)将每天准备收看奥运会直播不低于![]() 分钟的观众称为“超级奥运迷”,已知“超级奥运迷”中有
分钟的观众称为“超级奥运迷”,已知“超级奥运迷”中有![]()
名![]() 岁以上的观众,若从“超级奥运迷”中任意选取
岁以上的观众,若从“超级奥运迷”中任意选取![]() 人,求至少有
人,求至少有![]() 名
名![]() 岁以上的观众的概率.
岁以上的观众的概率.
附: 
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】截止到1999年底,我国人口约为13亿,若今后能将人口平均增长率控制在1%,经过x年后,我国人口为y(单位:亿).
(1)求y与x的函数关系式y=f(x);
(2)求函数y=f(x)的定义域;
(3)判断函数f(x)是增函数还是减函数,并指出函数增减的实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
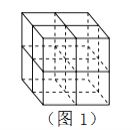
【题目】张师傅想要一个如图1所示的钢筋支架的组合体,来到一家钢制品加工店定制,拿出自己画的组合体三视图(如图2所示).店老板看了三视图,报了最低价,张师傅觉得很便宜,当即甩下定金和三视图,约定第二天提货.第二天提货时,店老板一脸坏笑的捧出如图3–1所示的组合体,张师傅一看,脸都绿了:“奸商,怎能如此偷工减料”.店老板说,我是按你的三视图做的,要不我给你加一个正方体,但要加价,随机加上了一个正方体,得到如图3–2所示的组合体;张师傅脸还是绿的,店老板又加上一个正方体,组成了如图 3–3 所示的组合体,又加价;张师傅脸继续绿,店老板再加一个正方体,组成如图 3–4 所示的组合体,再次加价;双方就三视图争吵不休……
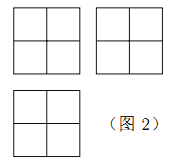
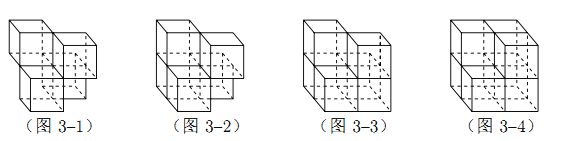
你认为店老板提供的![]() 个组合体的三视图与张师傅画的三视图一致的个数是( )
个组合体的三视图与张师傅画的三视图一致的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com