分析:(1)椭圆的长半轴长a=2,推出A(2,0),设椭圆E的方程为
+=1,由椭圆的对称性知|OC|=|OB|通过
•
=0,推出△AOC为等腰直角三角形,将C的坐标(1,1)代入椭圆方程得b椭圆E的方程;
(2)设在椭圆E上是否存点Q,使得|QB|
2-|QA|
2=2,说明直线经过椭圆内的点,判断点的个数即可.
(3)设点P(x
1,y
1),由M、N是⊙0的切点知,OM⊥MP,ON⊥NP,推出圆的方程,过椭圆E上异于其顶点的任一点P,作⊙O:x
2+y
2=
的两条切线,切点分别为M、N,求出直线MN在x轴、y轴上的截距分别为m、n,然后证明:
+
为定值.
解答:
解:(1)依题意知:椭圆的长半轴长a=2,则A(2,0),
设椭圆E的方程为
+=1-----------------------(2分)
由椭圆的对称性知|OC|=|OB|又∵
•
=0,|BC|=2|AC|
∴AC⊥BC,|OC|=|AC|∴△AOC为等腰直角三角形,
∴点C的坐标为(1,1),点B的坐标为(-1,-1),---------------------(4分)
将C的坐标(1,1)代入椭圆方程得b
2=
,
∴所求的椭圆E的方程为
+=1-----------------------------(5分)
(2)设在椭圆E上存在点Q,使得|QB|
2-|QA|
2=2,
设Q(x
0,y
0),则|QB|
2-|QA|
2=(x
0+1)
2+(y
0+1)
2-(x
0-2)
2-y
02=6x
0+2y
0-2=2,
即点Q在直线3x+y-2=0上,-----------------------------------------(7分)
∴点Q即直线3x+y-2=0与椭圆E的交点,
∵直线3x+y-2=0过点(
,0),而点椭圆(
,0)在椭圆E的内部,
∴满足条件的点Q存在,且有两个.-----------------------------------(9分)
(3)设点P(x
1,y
1),由M、N是⊙0的切点知,OM⊥MP,ON⊥NP,
∴O、M、P、N四点在同一圆上,-----------------------------------(10分)
且圆的直径为OP,则圆心为
(,),
其方程为
(x-)2+(y-)2=,----------------------(11分)
即x
2+y
2-x
1x-y
1y=0-----④
即点M、N满足方程④,又点M、N都在⊙O上,

∴M、N坐标也满足方程⊙O:x
2+y
2=
---------------⑤
⑤-④得直线MN的方程为x
1x+y
1y=
,------------------------------(12分)
令y=0得m=
,令x=0得n=
,------------------------(13分)
∴x
1=
,y
1=
,又点P在椭圆E上,
∴
()2+3()2=4,即
+
=
为定值.-----------------------(14分)

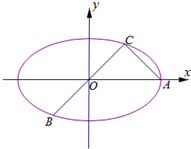 如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且
如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且


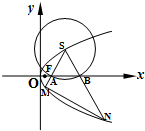 如图,已知点F是抛物线C:y2=x的焦点,S是抛物线C在第一象限内的点,且|SF|=
如图,已知点F是抛物线C:y2=x的焦点,S是抛物线C在第一象限内的点,且|SF|=