45和80的等比中项为±60．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

19．45和80的等比中项为±60．

分析直接利用等比中项的概念列式求值．

解答解：设45和80的等比中项为x，
则由等比中项的概念得：x²=45×80=3600，
∴x=±60．
故答案为：±60．

点评本题考查等比数列的通项公式，考查了等比中项的概念，是基础的计算题．

练习册系列答案

学府图书寒假作业系列答案

学段衔接提升方案赢在高考寒假作业系列答案

新校园快乐假期系列寒假生活指导系列答案

新思维寒假作业系列答案

新路学业寒假作业快乐假期新疆青少年出版社系列答案

新课堂假期生活假期作业寒假合编系列答案

新课程寒假作业广西师范大学出版社系列答案

新课程寒假作业本系列答案

新课标快乐提优寒假作业陕西旅游出版社系列答案

新课标寒假衔接系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

9．下列函数中x=0是极值点的函数是（　　）

A．

f（x）=-x³

B．

f（x）=x²

C．

f（x）=sinx-x

D．

f（x）=$\frac{1}{x}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

10．

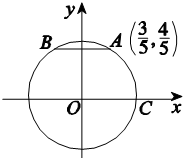如图所示，A，B是单位圆O上的点，且B在第二象限，C是圆与x轴正半轴的交点，A点的坐标为（$\frac{3}{5}$，$\frac{4}{5}$），且A与B关于y轴对称．
（1）求sin∠COA；
（2）求cos∠COB．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

7．已知{a_n}为等比数列，若a₁+a₄=8，a₃+a₆=2，则公比q的值为（　　）

A．

±2

B．

$±\frac{1}{2}$

C．

D．

$\frac{1}{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

14．

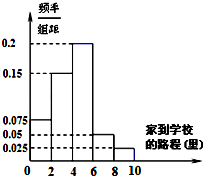某高中地处市区，学校规定家到学校的路程在10里以内的学生可以走读，因交通便利，所以走读生人数很多．该校学生会先后5次对走读生的午休情况作了统计，得到如下资料：
①若把家到学校的距离分为五个区间：[0，2）、[2，4）、[4，6）、[6，8）、[8，10），午休的走读生的分布情况如频率分布直方图所示；
②走读生是否午休与下午开始上课的时间有着密切的关系． 5次调查结果的统计表如表：

下午开始上课时间	2：10	2：20	2：30	2：40	2：50
平均每天午休人数	250	350	500	650	750

（1）若随机地调查一位午休的走读生，估计家到学校的路程（单位：里）在[2，6）的概率是多少？
（2）如果把下午开始上课时间2：10作为横坐标0，然后上课时间每推迟10分钟，横坐标x增加1，并以平均每天午休人数作为纵坐标y，试列出x与y的统计表，并根据表中的数据求平均每天午休人数$\widehat{y}$与上课时间x之间的线性回归方程$\widehat{y}$=bx+a；
（3）预测当下午上课时间推迟到3：00时，家距学校的路程在6里路以上的走读生中约有多少人午休？
（注：线性回归直线方程系数公式b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$．）

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

4．已知等比数列{a_n}的前n项和为S_n，且满足S₇=2，S₁₄=6，则S₂₁等于14．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

11．有一段演绎推理是这样的：“因为一次函数y=kx+b（k≠0）在R上是增函数，而y=-x+2是一次函数，所以y=-x+2在R上是增函数”的结论显然是错误，这是因为（　　）

A．

大前提错误

B．

小前提错误

C．

推理形式错误