
分析 (1)求得圆心到直线的距离,由弦长公式,计算即可得到r2=1,进而得到圆的方程;
(2)令切线方程为y-4=k(x-2),设$Q({x}_{1},{{x}_{1}}^{2}),R({x}_{2},{{x}_{2}}^{2}),PQ,PR$的斜率分别为k1、k2,求得直线QR的方程,运用直线和圆相切的条件,化简整理,再由圆心到直线QR的距离,即可判断所求位置关系.
解答 解:(1)∵C(0,2),∴圆心C到直线x-2y+2=0的距离为$d=\frac{{|{0-4+2}|}}{{\sqrt{5}}}=\frac{2}{{\sqrt{5}}}$,
∵截得的弦长为$\frac{{2\sqrt{5}}}{5}$,∴${r^2}={({\frac{2}{{\sqrt{5}}}})^2}+{({\frac{{\sqrt{5}}}{5}})^2}=1$,
∴圆C的方程为:x2+(y-2)2=1;
(2)令切线方程为y-4=k(x-2),从而$d=\frac{|2-2k|}{\sqrt{{k}^{2}+1}}=1$,即3k2-8k+3=0,
设$Q({x}_{1},{{x}_{1}}^{2}),R({x}_{2},{{x}_{2}}^{2}),PQ,PR$的斜率分别为k1、k2,
从而可得${k_1}•{k_2}=1,{k_1}+{k_2}=\frac{8}{3}$,
联立$\left\{\begin{array}{l}{y-4=k(x-2)}\\{y={x}^{2}}\end{array}\right.$,得(x-2)(x-k+2)=0,
∴x1=k1-2,x2=k2-2,
又由于直线QR的方程为$y-{{x}_{1}}^{2}=\frac{{{x}_{1}}^{2}-{{x}_{2}}^{2}}{{x}_{1}-{x}_{2}}(x-{x}_{1})$,
即y=(x1+x2)x-x1•x2=(k1+k2-4)x-(k1-2)(k2-2)
=(k1+k2-4)x-k1k2+2(k1+k2)-4=$-\frac{4}{3}x+\frac{1}{3}$.
∴4x+3y-1=0.
由圆心(0,2)到直线QR的距离为$\frac{|0+6-1|}{\sqrt{{4}^{2}+{3}^{2}}}=1$,从而可得直线与圆相切.
点评 本题考查直线和圆的位置关系,考查直线和圆相交的弦长公式和相切的条件:d=r,考查运算能力,属于中档题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{57}{7}$ | C. | 28 | D. | 31 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{1}{4}}]$ | B. | $[{-\frac{1}{4},+∞})$ | C. | $({-∞,-\frac{3}{4}}]$ | D. | $[{-\frac{3}{4},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
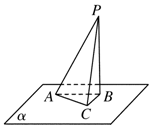 如图所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )
如图所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )| A. | 一条线段 | B. | 一条直线 | ||
| C. | 一个圆 | D. | 一个圆,但要去掉两个点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{17}$ | D. | $\frac{1}{18}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com