
【题目】定义在![]() 上的函数
上的函数![]() ,如果对任意的
,如果对任意的![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 为
为![]() 阶伸缩函数.
阶伸缩函数.
(![]() )若函数
)若函数![]() 为二阶伸缩函数,且当
为二阶伸缩函数,且当![]() 时,
时, ![]() ,求
,求![]() 的值.
的值.
(![]() )若
)若![]() 为三阶伸缩函数,且当
为三阶伸缩函数,且当![]() 时,
时, ![]() ,求证:函数
,求证:函数![]() 在
在![]() 上无零点.
上无零点.
(![]() )若函数
)若函数![]() 为
为![]() 阶伸缩函数,且当
阶伸缩函数,且当![]() 时,
时, ![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 在
在![]() 上的取值范围.
上的取值范围.
【答案】(1)1;(2)证明见解析;(3) ![]() .
.
【解析】试题分析:(Ⅰ)当x∈(1,2]时, ![]() ,从而f(
,从而f(![]() )=
)=![]() ,由此能求出函数f(x)为二阶伸缩函数,由此能求出
,由此能求出函数f(x)为二阶伸缩函数,由此能求出![]() 的值.
的值.
(Ⅱ)当x∈(1,3]时, ![]() ,由此推导出函数
,由此推导出函数![]() 在(1,+∞)上无零点.
在(1,+∞)上无零点.
(Ⅲ)当x∈(kn,kn+1]时, ![]() ,由此得到
,由此得到![]() ,当x∈(kn,kn+1]时,f(x)∈[0,kn),由此能求出f(x)在(0,kn+1](n∈N*)上的取值范围是[0,kn).
,当x∈(kn,kn+1]时,f(x)∈[0,kn),由此能求出f(x)在(0,kn+1](n∈N*)上的取值范围是[0,kn).
试题解析:
(Ⅰ)由题设,当x∈(1,2]时,![]() ,
,
∴![]() .
.
∵函数f(x)为二阶伸缩函数,
∴对任意x∈(0,+∞),都有f(2x)=2f(x).
∴![]() .
.
(Ⅱ)当x∈(3m,3m+1](m∈N*)时,![]() .
.
由f(x)为三阶伸缩函数,有f(3x)=3f(x)
∵x∈(1,3]时,![]() .
.
∴![]() .
.
令![]() ,解得x=0或x=3m,它们均不在(3m,3m+1]内.
,解得x=0或x=3m,它们均不在(3m,3m+1]内.
∴函数![]() 在(1,+∞)上无零点.
在(1,+∞)上无零点.
(Ⅲ) 由题设,若函数f(x)为k阶伸缩函数,有f(kx)=kf(x),
且当x∈(1,k]时,f(x)的取值范围是[0,1).
∴当x∈(kn,kn+1]时,![]() .
.
∵![]() ,所以
,所以![]() .
.
∴当x∈(kn,kn+1]时,f(x)∈[0,kn).
当x∈(0,1]时,即0<x≤1,
则k(k≥2,k∈N*)使![]() ,
,
∴1<kx≤k,即kx∈(1,k],∴f(kx)∈[0,1).
又![]() ,∴
,∴![]() ,即
,即![]() .
.
∵k≥2,
∴f(x)在(0,kn+1](n∈N*)上的取值范围是[0,kn).


科目:高中数学 来源: 题型:
【题目】试求下列函数的定义域与值域:
(1)f(x)=(x-1)2+1,x∈{-1,0,1,2,3};
(2)f(x)=(x-1)2+1;
(3)f(x)=![]() ;
;
(4)f(x)=x-![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
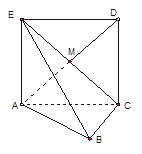
【题目】如图,边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M,![]() ,且AC=BC.
,且AC=BC.
(1)求证:![]() 平面EBC;
平面EBC;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个学生在一次竞赛中要回答![]() 道题是这样产生的:从
道题是这样产生的:从![]() 道物理题中随机抽取
道物理题中随机抽取![]() 道;从
道;从![]() 道化学题中随机抽取
道化学题中随机抽取![]() 道;从
道;从![]() 道生物题中随机抽取
道生物题中随机抽取![]() 道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为
道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为![]() ,化学题的编号为
,化学题的编号为![]() ,生物题的编号为
,生物题的编号为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线L的参数方程为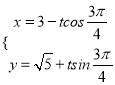 (
(![]() 为参数).在以原点
为参数).在以原点 ![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标中,圆C的方程为
轴正半轴为极轴的极坐标中,圆C的方程为![]() .
.
(Ⅰ)写出直线L的倾斜角![]() 和圆C的直角坐标方程;
和圆C的直角坐标方程;
(Ⅱ)若点 P坐标为![]() ,圆C与直线L交于 A,B两点,求|PA|
,圆C与直线L交于 A,B两点,求|PA|![]() |PB|的值.
|PB|的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l、m,平面α、β,下列命题正确的是 ( )
A. l∥β,lαα∥β
B. l∥β,m∥β,lα,mαα∥β
C. l∥m,lα,mβα∥β
D. l∥β,m∥β,lα,mα,l∩m=Mα∥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为![]() ,答对文科题的概率均为
,答对文科题的概率均为![]() ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() (其中
(其中![]() )满足下列3个条件:
)满足下列3个条件:
①函数![]() 的图象过坐标原点;
的图象过坐标原点;
②函数![]() 的对称轴方程为
的对称轴方程为![]() ;
;
③方程![]() 有两个相等的实数根,
有两个相等的实数根,
令![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求使不等式![]() 恒成立的实数
恒成立的实数![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com